SLAM

一个不起眼的烂笔头

Basic Knowledge & Small Talk & Some Problems

Posted by wykxwyc on March 21, 2019

目录

对相机内外参的简单理解

内参：三个量，焦距，成像平面上X/Y方向上的平移，X/Y方向上各自的缩放比例（或者说fx，fy，cx，cy两个焦距，两个平移），他们可以组成一个内参矩阵K。

外参:两个量，相机从世界坐标系转换到相机坐标系的旋转R以及平移t。

相机模型的推导

问题描述：已知世界坐标系下的一点 \(P\) ,相机的焦距为 \(f\) ,求相机成像平面上的点与世界坐标系中点的对应关系？

答案：
\(\left(\begin{array}{l}{u} \\ {v} \\ {1}\end{array}\right)=\frac{1}{Z}\left(\begin{array}{ccc}{f_{x}} & {0} & {c_{x}} \\ {0} & {f_{y}} & {c_{y}} \\ {0} & {0} & {1}\end{array}\right)\left(\begin{array}{l}{X} \\ {Y} \\ {Z}\end{array}\right) \triangleq \frac{1}{Z} \boldsymbol{K} \boldsymbol{P} \tag{5.6}\)

如果考虑世界坐标系下点的平移和旋转，并用齐次坐标系表示：
\(Z \boldsymbol{P}_{u v}=Z\left[\begin{array}{l}{u} \\ {v} \\ {1}\end{array}\right]=\boldsymbol{K}\left(\boldsymbol{R P}_{w}+\boldsymbol{t}\right)=\boldsymbol{K} \boldsymbol{T} \boldsymbol{P}_{w} \tag{5.8}\)

双目相机模型的推导

问题描述：根据给定的一个双目相机（基线长度 \(b\) 已知），求通过这个双目相机得到两幅图像后，如何知道物体的深度信息？

答案：
\(\begin{array}{c}{\frac{z-f}{z}=\frac{b-u_{L}+u_{R}}{b}} \\ {z=\frac{f b}{d}, \quad d=u_{L}-u_{R}}\end{array} \tag{5.15-5.16}\)

RGBD相机的实现原理
1)TOF技术

TOF(Time of Flight)，直译为飞行时间法。它的工作原理是通过给被测目标连续发送光脉冲，然后在传感器端接收从物体返回的光信号，最后通过计算发射和接收光信号的飞行（往返）时间来得到被测目标的距离。 与超声波测距不同的是超声波测距对反射物体要求比较高，面积小的物体，如线、锥形物体就基本测不到，而TOF对被测物体要求的尺寸、面积等要求更低，测距精度高、测距远、响应快。 与3D结构光相比，TOF技术发射的不是散斑，而是面光源，因此在一定距离内，TOF的光信息不会出现大量的衰减。其优势在于工作距离更远，适用于手机后置镜头。

事实上，无人驾驶中的激光雷达中也可以用到TOF技术，而用于消费型电子产品中的TOF相机主要由光源、感光芯片、镜头、传感器、驱动控制电路以及处理电路等几部分关键单元组成，TOF相机包括发射照明模块和感光接收模块两个核心部分。

2)3D结构光(三维结构光)

3D结构光技术是通过近红外激光器，将具有一定结构特征的光线投射到被摄物体上，再由专门的红外摄像头进行采集。这种具备一定结构的光线，会因被摄物体的不同深度区域，而采集不同的图像相位信息，然后通过运算单元将这种结构的变化换算成深度信息，获得三维结构。 TrueDepth 采用的就是结构光技术，即一种光解码技术，将光线结构化，将光线投射到物体上，形成畸变，然后另一个摄像机对畸变进行捕捉，通过三角法测量原理获得三维成像，结构光方案功耗低、精度高，对于近距离人脸识别来说，具备应用优势。

径向畸变和切向畸变

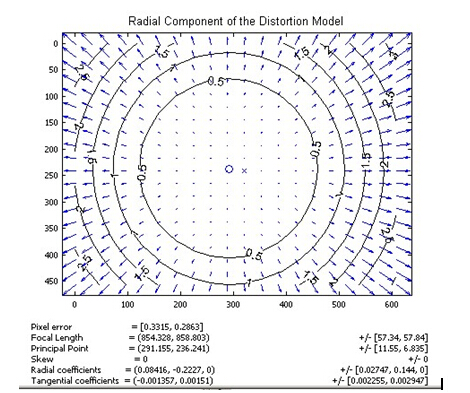
r_distorted 径向畸变:与相机中心点距离r有关，距离越远，畸变(变小/变大)越多。本质与透镜形状有关。

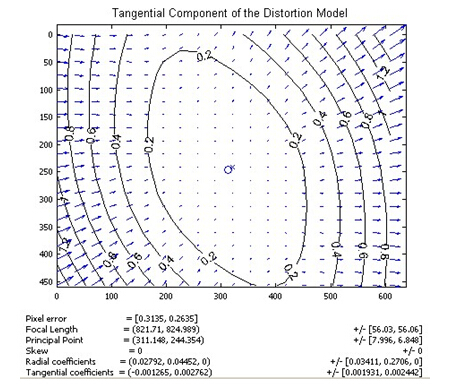
t_distorted 切向畸变:沿着某个过一基点的向量方向上，与基点的垂直距离越大，畸变越大。本质与透镜的安装位置有关。

参考链接：https://blog.csdn.net/dcrmg/article/details/52950141

图像金字塔

图像金字塔解决的问题是角点不具有方向性和尺度的弱点，《SLAM十四讲》page135，

灰度质心法

灰度质心法解决的问题是特征的旋转问题，使特征具有方向性，《SLAM十四讲》page135，特征提取

汉明距离（Hamming distance）

两个二进制串之间不同位数的个数，用于衡量两个特征的描述子之间的差异。

快速近似最近邻（FLANN）
光流法的Coarse-to-fine optical flow estimation
简要叙述LeGO-LOAM和LOAM的原理，以及他们之间的共同点和区别

LeGO-LOAM是一种可以运行在嵌入式板卡上的轻量级雷达里程计和建图算法。
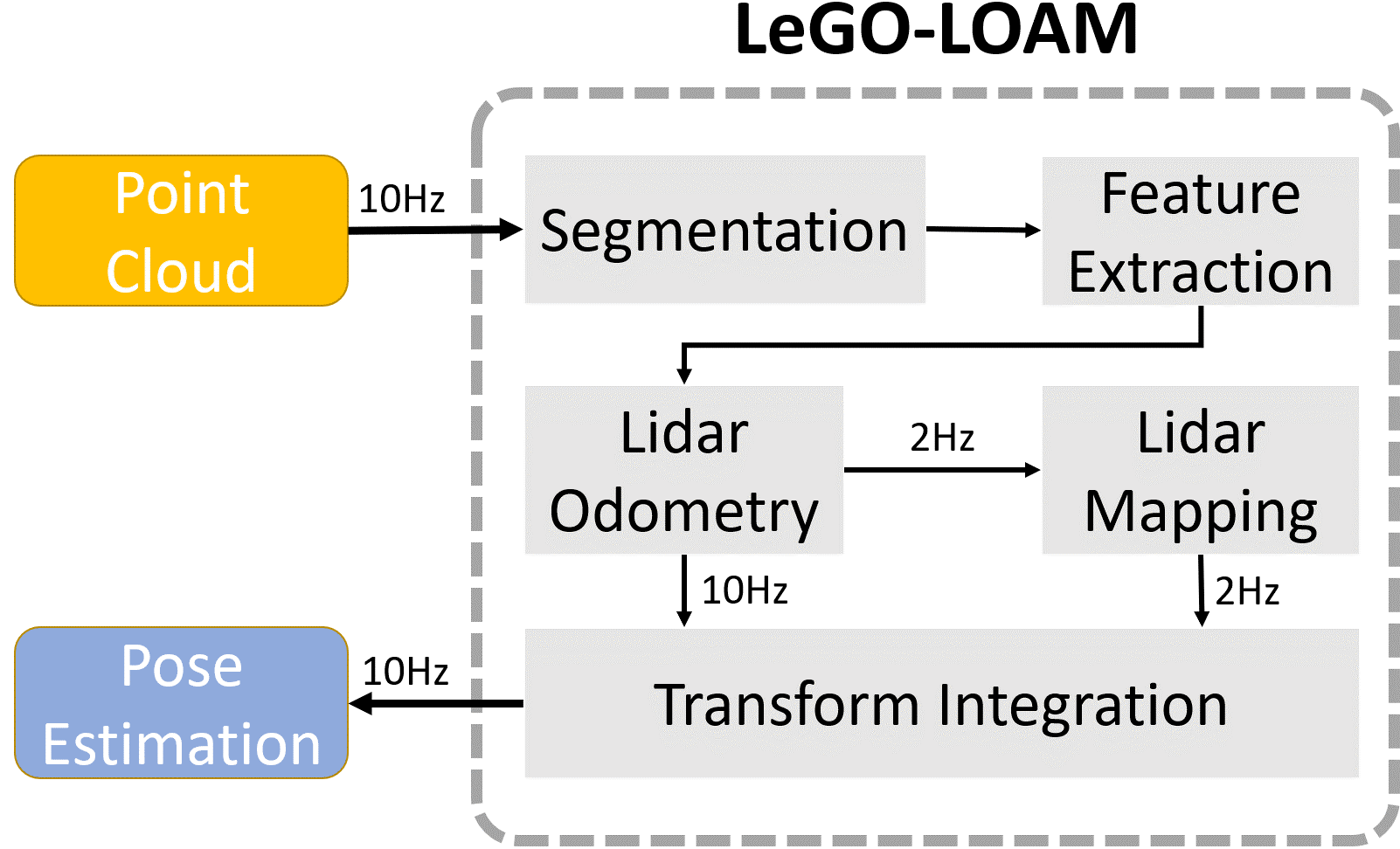
它主要分为5个模块，分别是点云分割，特征提取，雷达里程计，雷达建图和变换融合。 lego-loam-system-organization

点云分割模块通过降采样、标记点的类型、忽略数量过少的点来减少后面的计算量，提高速度。

特征提取模块通过计算点的粗糙度，从地面点和分段点中提取特征。这种特征提取方法和LOAM十分类似。

雷达里程计通过估计两次连续扫描来估计传感器的运动，这个模块相比于LOAM有2个创新点：特征的匹配加上了标签以及两步L-M优化。先通过地面匹配得到竖直方向上的平移和Roll和Pitch角。然后再匹配特征边得到x，y方向平移和yaw角。

雷达建图主要是结合雷达里程计的变换，将特征注册到全局点云地图上。

变换融合主要将新特征匹配到已有的地图上，以较低的频率运行，并进行L-M位置优化，输出最终姿态估计。

真阳性(TP),假阳性(FP),真阴性(TN),假阴性(FN),准确率,召回率的含义

准确率:
\(precision=\frac{TP}{TP+FP}\)
真正检测出来的真阳性占总体检测出来阳性的比例，从检测方的角度来看。

召回率:
\(recall=\frac{TP}{TP+FN}\)
真正检测出来的真阳性占实际总阳性的比例，从被检测方的角度来看。

什么是分支定界法（branch and bound algorithm）？

分支定界算法的定义：
对有约束条件的最优化问题（其可行解为有限数）的所有可行解空间恰当地进行系统搜索，这就是分支与界定的内容。
通常把全部解空间反复地分割为越来越小的子集，称为分枝。
对每个子集内的解集计算一个目标下界（对于最小值问题），这称为定界。
在每次分枝后，若某个已知可行解集的目标值不能达到当前的界限，则将这个子集舍去。这样，许多子集不予考虑，这称为剪枝。这就是分枝界限法的思路。

  • 分支定界算法的一个例子：用分支定界法求背包问题。
    问题：一个容量为10的集装箱，有重量分别为4,8,5的货物，如何才能装最多？
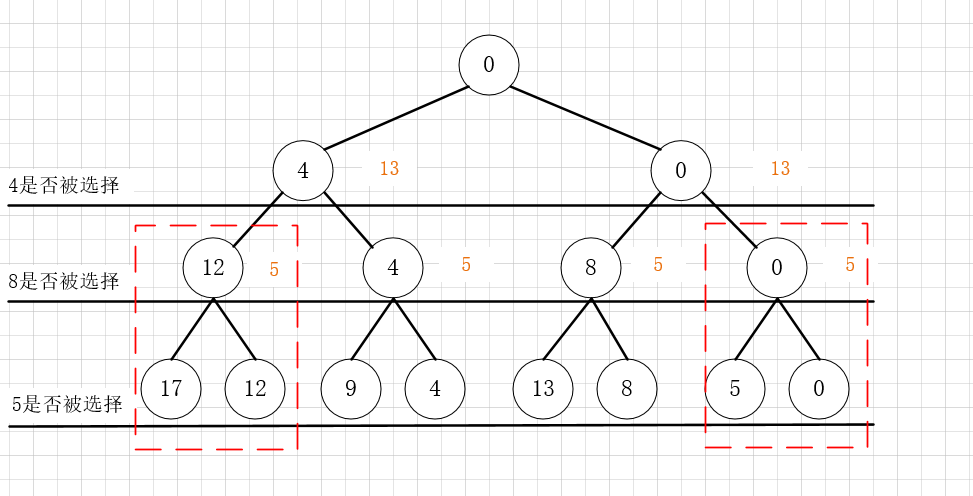
    branch-and-bound

FIFO算法：
1.首先定义best=0.
2.第一层，4被选择，此时的best修改成4，加入到队列中；0<best 计算0节点的最大期望，13>best，加入到队列中。
3.第二层，8被选择，12>10，截枝；4=best，加入到队列中；8>best, 加入到队列，修改best=8，0节点的最大期望<best，截枝；
4.第三层，修改best即可。

参考链接：
https://www.cnblogs.com/xiaofanke/p/9498820.html
https://www.cnblogs.com/sage-blog/p/3917836.html

对占据栅格地图的理解（Occupancy Grid Map）

地图是激光 slam 系统的核心，通常激光 slam 都采用 logodds 算法对栅格地图进行概率更新。知乎上有个人对 Coursera 上课笔记进行了总结，写得非常好，对公式的推导很简洁。 https://zhuanlan.zhihu.com/p/21738718

李群和李代数

SO(3)是特殊正交群，Special Orthogonal group，里面的元素是旋转矩阵R，大写SO(3)的李代数为小写so(3),里面的元素是向量a，两者的关系：R=exp(a^);

SE(3)是特殊欧式群，Special Euclidean group，里面的元素是齐次变换矩阵T，既有旋转又有平移，旋转R是SO(3)中的元素，平移是三维列向量t。 大写SE(3)的李代数是小写se(3)，里面的元素是六维向量，前三维平移，后三维旋转，旋转的元素是so(3)内的。

李群和李代数中需要记住的基本公式

运算符 \(^{\wedge}\) 和运算符 \(^{\vee}\) 的定义：

\[a^{\wedge}=A=\left[ \begin{array}{ccc}{0} & {-a_{3}} & {a_{2}} \\ {a_{3}} & {0} & {-a_{1}} \\ {-a_{2}} & {a_{1}} & {0}\end{array}\right], \quad A^{\vee}=a\]
2D-2D(对极几何)：本质矩阵,基础矩阵，单应性矩阵是什么？表示了什么含义？如何求解？

这三个矩阵都是2D-2D中，通过相机的图像估计相机运动的矩阵。

本质矩阵（Essential Matrix）

本质矩阵由对极约束定义，含义就是两帧图像之间的平移向量计算的反对称阵t^乘以旋转矩阵R计算得到的矩阵，即E=t^R。

本质矩阵表达的是路标P在不同的相机位姿中转换到归一化平面上上的坐标x1和x2应该满足的关系，也就是x2^(T)·E·x1=0。

空间物体有6个自由度，减去E的一个尺度等价性，所以E应该有5个自由度，由5对点就可以求解。但这样求解涉及E内在的非线性性质，不如直接求解矩阵E的9个量，考虑到E还有一个尺度等价性，所以通过8个方程，8点法就能求解E。(当然最后还要考虑E的内在性质，奇异值要符合要求，还要进行调整)。

基础矩阵(Fundamental Matrix)

基础矩阵的定义就是在本质矩阵E的基础上，左边乘以K^(-T),右边乘以K^(-1)。

基础矩阵表达的含义是两幅不同图像中的两个对应像素点p1和p2之间的约束，也就是p2^(T)·F·p1=0的约束关系。

因为相机的内参K一般都是已知的，所以只要根据求解的本质矩阵E，再由F=K^(-T)·E·K^(-1)。

单应性矩阵（Homography）

单应矩阵表达的含义是两幅不同图像中的两个对应像素点p1和p2之间的约束，p1和p2代表的实际物体点在同一个平面上。用数学表达式描述就是H=K·(R-t·n^(T)/d)·K^(-1)。

单应矩阵通常描述处于共同平面上的一些点在两张图像之间的变换关系，也就是p2=H·p1。

因为H也是一个3x3的矩阵，因此一共有9个量需要求。又因为p2=H·p1，根据这个公式代入相应的点求解就可以了，但是我们需要多少对点呢？因为所提供的点的Z上的分量为1，是一个齐次坐标系下的，因此每一个点对只能提供x，y方向上的两个约束，考虑到H少一个尺度分量，因此是8个自由度的，因此只要通过4对点就能确定H。

3D-2D：PnP求解相机运动R和t

PnP（Perspective-n-Point）是求解3D到2D点对运动的方法。它的主要内容通俗来说就是，当我知道以前一些点在3D空间中的位置(3D位置通过以前的2D图像求解得到)，现在又通过相机观测到了照片，如何通过这张2D照片估计相机的位姿。

直接线性变换(DLT)

使用齐次坐标计算方程s[p1]=[R|t]·[P]，求解[R|t]。每一对点会提供2个约束。因为[R|t]一共有12个未知量，所以只要6对点就可以求解出闭式解。

SVD方法

用SVD可以很容易得到任意矩阵的满秩分解，用满秩分解可以对数据做压缩。
可以用SVD来证明对任意M*N的矩阵均存在如下分解：
\(A_{m \times n} \Rightarrow X_{m \times k} Y_{k \times n} \tag{SVD-1}\) 其中： \(k=rank(A) \tag{SVD-2}\)

关于使用SVD的例子:
SVD SVD

P3P

利用3对匹配点求解PnP的问题。3对点构成了一个三棱锥,一共有3个侧面，3个余弦定理构成3个方程。化简方程后得到两个比值x和y,然后求解得到旋转R和平移t。问题是如何从x和y求解R和t?

3D-3D:ICP

ICP的求解方法有两种：

  • SVD：
    求解闭式解的方法。主要思想是分离R和t，先求R，再求t。

  • 非线性优化的方法：
    用迭代的方法去求总体误差最小的解，当误差在我认为允许的范围内了之后就认为可行了。

直接法是什么？有什么意义？如何计算？

不使用特征点，而直接使用图像的灰度信息来计算相机的运动。

逆深度是什么？作用是什么？
深度滤波器是什么？用在什么方面？
  • 深度滤波器及其技术
    当知道了某个像素在各张照片中的位置，我们可以用三角测量确定它的深度。将深度假设为满足某种概率分布，我们通过很多次三角测量让深度估计收敛，让深度从一个很不确定的量收敛到一个稳定值，这就是深度滤波器技术。对应这个概率分布假设的滤波器就是深度滤波器,如高斯分布的深度滤波器。
harris角点是什么？以及它如何实施？
手推本质矩阵和单应矩阵的公式
状态估计中批量式和渐进式的区别

  • 批量式（Batch） 在后端优化中，通常考虑一段更长时间内（或所有时间内）的状态估计问题，不但使用过去的信息更新自己的状态，也使用未来的信息更新自己。

  • 渐进式（Incremental） 当前的状态只由过去的时刻决定，设置只由一个时刻决定，称之为渐进式。

经典SLAM模型的定义以及含义

经典 SLAM 模型，它由一个状态方程和一个运动方程构成：
\(\left\{\begin{array}{l}{\boldsymbol{x}_{k}=f\left(\boldsymbol{x}_{k-1}, \boldsymbol{u}_{k}\right)+\boldsymbol{w}_{k}} \\ {\boldsymbol{z}_{k, j}=h\left(\boldsymbol{y}_{j}, \boldsymbol{x}_{k}\right)+\boldsymbol{v}_{k, j}}\end{array}\right. \tag{6.1}\)
上式中：
\(\boldsymbol{x}_{k}\) 是相机的真实位姿；
\(u_{k}\) 是输入的运动数据；
\(\boldsymbol{w}_{k}\) 是运动方程的噪声；
\(\boldsymbol{z}_{k, j}\) 是通过观测得到的当前的位姿；
\(y_{j}\) 是路标点；
\(\boldsymbol{v}_{k, j}\) 是观测方程的噪声。

LiDAR与相机数据的融合

记录一个参考链接：
Fusion of Velodyne and Camera Data for Scene Parsing

Heyijia写的粒子滤波器(经过其他人合并)

https://blog.csdn.net/piaoxuezhong/article/details/78619150 s

罗德里格斯公式的推导过程

罗德里格斯公式(Rodrigues’s Formula)的推导过程：
简单来说就是一个待旋转向量绕着一个旋转轴旋转一个theta的角度。如何用旋转矩阵的形式将这个旋转表示出来？
分为如下几步：
1.将带旋转的向量分为与旋转轴平行的以及与旋转轴垂直的两个向量。
2.与旋转轴垂直的向量旋转theta的角度，平行的那部分保持不动。
3.将两部分加起来，就能得到最后旋转的结果了。
4.最后将这个结果中的原向量提取出来放在等式右边，原向量左乘了一个系数，这个系数就是罗德里格斯公式的旋转矩阵R。

参考链接：
罗德里格斯旋转公式推导

3张图说完KF的公式及推导

截取自bilibili视频机器学习-白板推导系列（十六）-粒子滤波（Particle Filter）

  • 1.问题的说明
    需要说明的是，图中的z代表的是真实值，x代表的是观测值，与我们往常所用的标记符号不同。
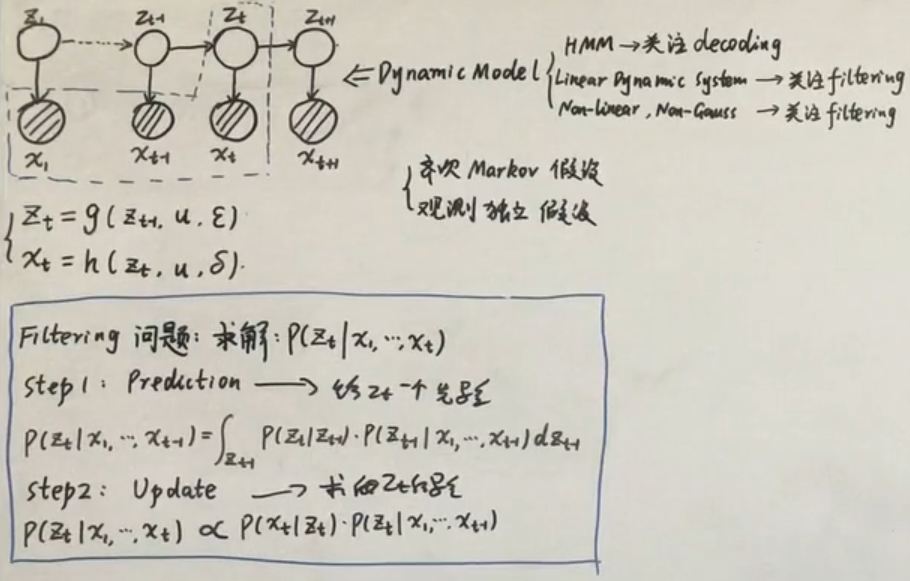
    problem

  • 2.预测过程
    prediction

  • 3.更新过程
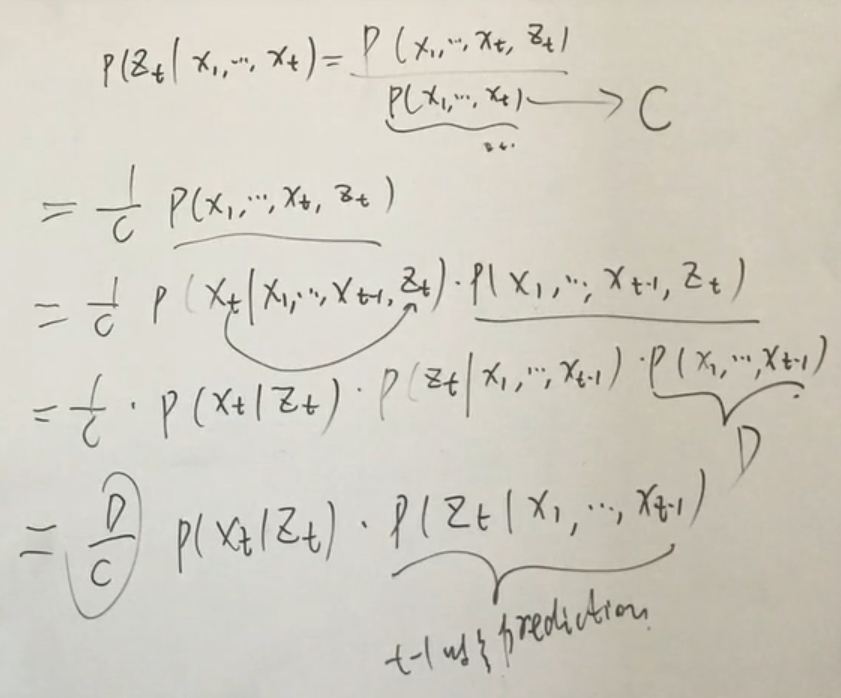
    update

梯度，雅克比，Hessian矩阵辨析

首先定义一个几个不同的函数：

  • 一个多元函数与标量的映射(自变量多维，因变量一维)：
    \(x=f\left(\theta_{1}, \theta_{2}, \theta_{3}\right)=f(\mathbf{q}) \tag{H-1}\)

  • 一个多元函数与向量的映射(自变量是多维，因变量多维) \(\mathbf{X}=\left[\begin{array}{l}{x} \\ {y}\end{array}\right]=\left[\begin{array}{l}{f_{1}(\mathbf{q})} \\ {f_{2}(\mathbf{q})}\end{array}\right] \tag{H-2}\)

1.梯度
对于公式H-1中的函数而言，一阶导数就是这个函数的梯度
\(\begin{array}{l}{\dot{x}=\nabla f \dot{\mathbf{q}}, \text { where } \nabla f \in \mathfrak{R}^{1 \times 3}} \\ {\nabla f=\left[\begin{array}{lll}{\frac{\partial f}{\partial \theta_{1}}} & {\frac{\partial f}{\partial \theta_{2}}} & {\frac{\partial f}{\partial \theta_{3}}}\end{array}\right]}\end{array} \tag{H-3}\)

2.雅克比
对于公式H-2中的函数，一阶导数为雅克比矩阵
\(\dot{\mathbf{X}}=\mathbf{J} \dot{\mathbf{q}}=\left[\begin{array}{c}{\nabla f_{1}} \\ {\nabla f_{2}}\end{array}\right] \dot{\mathbf{q}}=\left[\begin{array}{ccc}{\frac{\partial f_{1}}{\partial \theta_{1}}} & {\frac{\partial f_{1}}{\partial \theta_{2}}} & {\frac{\partial f_{1}}{\partial \theta_{3}}} \\ {\frac{\partial f_{2}}{\partial \theta_{1}}} & {\frac{\partial f_{2}}{\partial \theta_{2}}} & {\frac{\partial f_{2}}{\partial \theta_{3}}}\end{array}\right] \dot{\mathbf{q}} \tag{H-4}\)

对公式H-2中的函数，二阶导数为机器人的Hessian矩阵
\(\ddot{\mathbf{X}}=\mathbf{J} \ddot{\mathbf{q}}+\mathbf{j}_{\mathbf{q}}=\mathbf{J} \ddot{\mathbf{q}}+\dot{\mathbf{q}}^{\top} *[\mathbf{H}] \dot{\mathbf{q}}=\mathbf{J} \ddot{\mathbf{q}}+\left[\begin{array}{c}{\dot{\mathbf{q}}^{\top} \mathbf{J}\left(\nabla f_{1}\right)} \\ {\dot{\mathbf{q}}^{\top} \mathbf{J}\left(\nabla f_{2}\right)}\end{array}\right] \dot{\mathbf{q}}=\mathbf{J} \ddot{\mathbf{q}}+\left[\begin{array}{c}{\dot{\mathbf{q}}^{\top} \mathbf{H}_{1}} \\ {\dot{\mathbf{q}}^{\top} \mathbf{H}_{2}}\end{array}\right]_{2 \times 3} \dot{\mathbf{q}} \tag{H-5}\)

其中：
\(\mathbf{H}_{1}=\left[\begin{array}{ccc}{\frac{\partial^{2} f_{1}}{\partial \theta_{1}^{2}}} & {\frac{\partial^{2} f_{1}}{\partial \theta_{1} \partial \theta_{2}}} & {\frac{\partial^{2} f_{1}}{\partial \theta_{1} \partial \theta_{3}}} \\ {\frac{\partial^{2} f_{1}}{\partial \theta_{1} \partial \theta_{2}}} & {\frac{\partial^{2} f_{1}}{\partial \theta_{2}^{2}}} & {\frac{\partial^{2} f_{1}}{\partial \theta_{2} \partial \theta_{3}}} \\ {\frac{\partial^{2} f_{1}}{\partial \theta_{1} \partial \theta_{3}}} & {\frac{\partial^{2} f_{1}}{\partial \theta_{2} \partial \theta_{3}}} & {\frac{\partial^{2} f_{1}}{\partial \theta_{3}^{2}}}\end{array}\right]_{3 \times 3} \tag{H-6}\)

\[\mathbf{H}_{2}=\left[\begin{array}{ccc}{\frac{\partial^{2} f_{2}}{\partial \theta_{1}^{2}}} & {\frac{\partial^{2} f_{2}}{\partial \theta_{1} \partial \theta_{2}}} & {\frac{\partial^{2} f_{2}}{\partial \theta_{1} \partial \theta_{3}}} \\ {\frac{\partial^{2} f_{2}}{\partial \theta_{1} \partial \theta_{2}}} & {\frac{\partial^{2} f_{2}}{\partial \theta_{2}^{2}}} & {\frac{\partial^{2} f_{2}}{\partial \theta_{2} \partial \theta_{3}}} \\ {\frac{\partial^{2} f_{2}}{\partial \theta_{1} \partial \theta_{3}}} & {\frac{\partial^{2} f_{2}}{\partial \theta_{2} \partial \theta_{3}}} & {\frac{\partial^{2} f_{2}}{\partial \theta_{3}^{2}}}\end{array}\right]_{3 \times 3} \tag{H-7}\]

3.Hessian矩阵
对公式H-1中的函数，二阶导数为广义的Hessian 矩阵(这里的Hessian矩阵是对梯度求雅克比矩阵)
\(\begin{array}{ll}{\ddot{x}=\nabla f \ddot{\mathbf{q}}+\dot{\mathbf{q}}^{\top} \mathbf{J}(\nabla f)^{\top} \dot{\mathbf{q}}=\nabla f \ddot{\mathbf{q}}+\dot{\mathbf{q}}^{\top} \mathbf{H} \dot{\mathbf{q}}, \text { where } \mathbf{H} \in \mathfrak{R}^{3 \times 3}} \\ {\mathbf{H}=\left[\begin{array}{ccc}{\frac{\partial^{2} f}{\partial \theta_{1}^{2}}} & {\frac{\partial^{2} f}{\partial \theta_{1} \partial \theta_{2}}} & {\frac{\partial^{2} f}{\partial \theta_{1} \partial \theta_{3}}} \\ {\frac{\partial^{2} f}{\partial \theta_{1} \partial \theta_{2}}} & {\frac{\partial^{2} f}{\partial \theta_{2}^{2}}} & {\frac{\partial^{2} f}{\partial \theta_{2} \partial \theta_{3}}} \\ {\frac{\partial^{2} f}{\partial \theta_{1} \partial \theta_{3}}} & {\frac{\partial^{2} f}{\partial \theta_{2} \partial \theta_{3}}} & {\frac{\partial^{2} f}{\partial \theta_{3}^{2}}}\end{array}\right]}\end{array} \tag{H-8}\)

对于公式H-2中的函数，二阶导数在公式H-5中表示出来了，这里再重复写一遍：
\(\ddot{\mathbf{X}}=\mathbf{J} \ddot{\mathbf{q}}+\mathbf{j}_{\mathbf{q}}=\mathbf{J} \ddot{\mathbf{q}}+\dot{\mathbf{q}}^{\top} *[\mathbf{H}] \dot{\mathbf{q}}=\mathbf{J} \ddot{\mathbf{q}}+\left[\begin{array}{c}{\dot{\mathbf{q}}^{\top} \mathbf{J}\left(\nabla f_{1}\right)} \\ {\dot{\mathbf{q}}^{\top} \mathbf{J}\left(\nabla f_{2}\right)}\end{array}\right] \dot{\mathbf{q}}=\mathbf{J} \ddot{\mathbf{q}}+\left[\begin{array}{c}{\dot{\mathbf{q}}^{\top} \mathbf{H}_{1}} \\ {\dot{\mathbf{q}}^{\top} \mathbf{H}_{2}}\end{array}\right]_{2 \times 3} \dot{\mathbf{q}} \tag{H-5}\)
其中：
\([\mathbf{H}]\) 是真正我们所说的Hessian矩阵，它里面的分项\(\mathbf{H}_{1}\) 以及 \(\mathbf{H}_{2}\) 是上面说的广义的Hessian矩阵。
整个机器人的海森矩阵 \([\mathbf{H}] \in \mathfrak{R}^{2 \times 3 \times 3} \in \mathfrak{R}^{6 \times 3}\) 是这两个广义Hessian矩阵构成的，因此不能直接进行代数运算，也就是不能写成 \(\dot{\mathbf{q}}^{\top}[\mathbf{H}]\)

参考链接：
Hessian matrix-知乎

谭平《从相机标定到SLAM》中的问题
  • 确定空间二次曲线需要多少个点？一个圆和一条无穷远直线相交的条件如何求？
  • （谭平 The Circular Points on a 2D Plane)
  • Zhang Zhengyou相机标定每次求出两个Circular Point，通过6个Circular Point求得Absolute Conic标定
对一个点/向量/平面进行坐标系变换的公式表示？
PCA

[PCA]https://blog.csdn.net/program_developer/article/details/80632779

FEATURED TAGS
SLAM LeGO-LOAM C++ OS Database Redis
FRIENDS