LOAM是CMU的Zhang Ji在2014年提出来的三维激光雷达里程计建图算法,建图较为稀疏,主要通过提取特征边缘和特征平面进行匹配进行。算法在当时达到了state of art 的效果,算法过程简单并且效率很高,到现在为止,LOAM和V-LOAM也还是在KITTI排行榜上位居榜首的建图算法。
目录
摘要
方法
Loam采用的方法是使用一个2维雷达以6自由度移动进行建图。
面对的主要问题
不同时间收到的距离数据,以及运动估计造成的误差会造成点云数据误读。
主要思想
SLAM问题,用两个算法进行:
一个算法用高频但以低保真度估计雷达运动速度。
另一个算法以低频进行匹配和注册点云数据。
1.INTRODUCTION
略
2.RELATED WORK
略
3.注记与任务描述
- 解决的问题
通过3D雷达接收到的点云数据进行运动估计以及建图。 -
前提条件
雷达已经校准,雷达的角度以及线速度是平滑并且连续的,没有激变。 - 右上角表示坐标系
- 一次sweep定义
雷达完成一次scan coverage - 右下标k
\(k \in Z^{+}\) 代表第k次sweep
\(P_{k}\)
:第
\(k\)
次sweep时接收到的点云数据;
\(X_{(k, i)}^{L}\)
:
\(P_{k}\)
中的点𝑖
\(i\)
,在本地坐标系
\(\left\{L_{k}\right\}\)
中的坐标;
\(X_{(k, i)}^{W}\)
:
\(P_{k}\)
中的点
\(i\)
,在全局坐标系
\(\left\{W_{k}\right\}\)
中的坐标;
- 任务描述
给出一序列雷达点云 \(P_{k},k \in Z^{+}\) 计算每次雷达sweep中的雷达自运动,同时用点云数据 \(P_{k}\) 为刚遍历过的环境建立一张地图。
4.系统概述
A.雷达硬件
略
B.系统软件概述
\(\hat{P}\)
:雷达一次scan中接收到的数据,每一次sweep中,
\(\hat{P}\)
在
\(\{L\}\)
中注册,最后在第k次sweep组合起来的点云组成
\(P_{k}\)
;
Lidar odometry 接收点云数据,计算两连续sweep之间的雷达的运动,估计的运动被用于校正
\(P_{k}\)
中的失真。
组成框图:
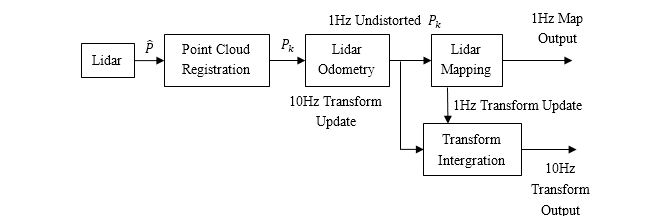
5.雷达里程计
A.特征点抽取
特征点的抽取根据以下公式进行:
\(c=\frac{1}{|S| \cdot\left\|X_{(k, i)}^{L}\right\|}\left\|\sum_{j \in s, j \neq i}\left(X_{(k, i)}^{L}-X_{(k, j)}^{L}\right)\right\| \tag{1}\)
式中:
\(i\)
表示
\(P_{k}\)
中的一个点,
\(i \in P_{k}\)
;
\(S\)
表示雷达在同一个scan中返回的一系列连续点𝑖
\(i\)
;
c值表示平面的光环程度,c值越小越平坦,选取其中c值最小的作为特征平面,选取其中c值最大的作为特征边缘。
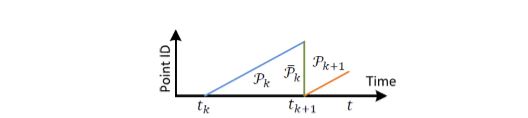
上图中,重投影点云到一次sweep的末尾。蓝线分块代表在第k扫时收到的点云。在第k扫结尾,
\(P_{k}\)
被重投影到时间戳
\(t_{k+1}\)
,重投影后我们得到
\(\overline{P}_{k}\)
(用绿色线段表示)。在第k+1扫,
\(\overline{P}_{k}\)
和新收到的点云
\(P_{k+1}\)
(橙色)一起被用来估计雷达运动。
B.找到特征点的对应关系
Odometry 算法估计一个sweep中的雷达运动。
\(t_{k}\)
sweep k的开始时间;
在每一个sweep结束后,接收到的点云数据
\(P_{k}\)
,被重投影到时间戳
\(t_{k+1}\)
上,重投影的点云表示为
\(\overline{P}_{k}\)
。
\(\overline{P}_{k}\)
与sweep k+1时接收到的点云数据
\(P_{k+1}\)
一起被用来估计雷达运动。
\(\varepsilon_{k+1}\)
:代表边沿点集(sets of edge points);
\(\mathcal{H}_{k+1}\)
:代表平面点集(sets of planar points);
在 \(\overline{P}_{k}\) 中,我们寻找边沿线对应于 \(\varepsilon_{k+1}\) 内部分点,寻找平面块对应于 \(\mathcal{H}_{k+1}\) 中的部分平面。
开始第k+1次sweep时,
\(P_{k+1}\)
为空,当越来越多的点被接收到时,
\(P_{k+1}\)
不断增大。
每次迭代,
\(\varepsilon_{k+1}\)
和
\(\mathcal{H}_{k+1}\)
通过使用当前的位姿变换被重投影到该sweep的起始时刻。
\(\tilde{\mathcal{E}}_{k+1}\)
和
\(\tilde{\mathcal{H}}_{k+1}\)
是重投影的点集。对于
\(\tilde{\mathcal{E}}_{k+1}\)
和
\(\tilde{\mathcal{H}}_{k+1}\)
中的每个点,我们找到
\(\overline{P}_{k}\)
中与它最邻近的点。为便于检索,
\(\overline{P}_{k}\)
存放在一个三维KD-tree中。
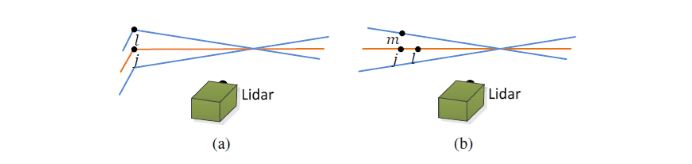
上图为寻找与 \(\tilde{\mathcal{E}}_{k+1}\) 中edge point对应的边缘线以及寻找与 \(\tilde{\mathcal{H}}_{k+1}\) 中planar point对应的平面片的过程。在(a)和(b)中,j是 \(\overline{P}_{k}\) 中与特征点最近的点。橙色线条代表与j相同的一次scan,蓝色线条代表两次连续scan。为了找到(a)中的edge line correspondence,先找到在蓝色线条上的另外1个点l,对应关系表示为(j,l)。为了找到(b)中的planar patch correspondence,先找到在蓝色线条上的另外2个点l和m,l在橙色线条上,m在蓝色线条上,对应关系表示为(j,l,m)。
找边缘线的过程:
i是
\(\tilde{\mathcal{E}}_{k+1}\)
中的一个点,
\(i \in \tilde{\mathcal{E}}_{k+1}\)
;
j是
\(\overline{P}_{k}\)
中i的最近点,
\(j \in \overline{P}_{k}\)
;
l是连续2个scan(j的下一扫)中距离i的最近点,(j,l)组成了与i点的对应,然后我们计算c值以检查其光滑性。
我们通过以下公式计算点到线的距离:
\(d_{\mathcal{E}}=\frac{\left|\left(\tilde{X}_{(k+1, i)}^{L}-\overline{X}_{(k, j)}^{L}\right) \times\left(\tilde{X}_{(k+1, i)}^{L}-\overline{X}_{(k, l)}^{L}\right)\right|}{\left|\overline{X}_{(k, j)}^{L}-\overline{X}_{(k, l)}^{L}\right|} \tag{2}\)
其中:
\(\tilde{X}_{(k+1, i)}^{L}, \overline{X}_{(k, j)}^{L}, \overline{X}_{(k, l)}^{L}\)
分别表示点𝑖,𝑗,𝑙在本地坐标系
\(\{L\}\)
中的坐标,
\(i \in \tilde{\varepsilon}_{k+1}, j, l \in \overline{P}_{k}\)
。
找平面块的过程:
i是
\(\tilde{\mathcal{H}}_{k+1}\)
中的一个点,
\(i \in \tilde{\mathcal{H}}_{k+1}\)
;
j是
\(\overline{P}_{k}\)
中i的最近点,
\(j \in \overline{P}_{k}\)
;
l,m是i的最近点,l与j在同一scan中,m在j的下一scan中,这保证了l,m,j三点是不共线的。为了验证l,m,j三点是平面点,然后我们计算c值以检查其光滑性。
通过以下公式计算点到平面的距离:
\(d_{\mathcal{H}}=\frac{\left|\left(\tilde{X}_{(k+1, i)}^{L}-\overline{X}_{(k, j)}^{L}\right)\left(\left(\overline{X}_{(k, j)}^{L}-\overline{X}_{(k, l)}^{L}\right) \times\left(\overline{X}_{(k, j)}^{L}-\overline{X}_{(k, m)}^{L}\right)\right)\right|}{\left|\left(\overline{X}_{(k, j)}^{L}-\overline{X}_{(k, l)}^{L}\right) \times\left(\overline{X}_{(k, j)}^{L}-\overline{X}_{(k, m)}^{L}\right)\right|} \tag{3}\)
其中:
\(\overline{X}_{(k, m)}^{L}\)
是点m在本地坐标系
\(\{L\}\)
中的坐标。
C.运动估计
假设:雷达一个sweep之中具有常数角度和线速度。
t是当前时间戳;
\(t_{k+1}\)
是sweep k+1的开始时间;
\(T_{k+1}^{L}\)
是
\(\left[t_{k+1}, t\right]\)
间的位姿变换,
\(T_{k+1}^{L}\)
包含6自由度,
\(T_{k+1}^{L}=\left[t_{x}, t_{y}, t_{z}, \theta_{x}, \theta_{y}, \theta_{z}\right]^{T}\)
;
给定点
\(i, i \in P_{k+1}, t_{i}\)
是其时间戳,
\(T_{(k+1, i)}^{L}\)
是
\(\left[t_{k+1}, t_{i}\right]\)
之间的位姿变换,通过线性插补
\(T_{k+1}^{L}\)
我们可以得到
\(T_{(k+1, i)}^{L}\)
,公式如下:
\(T_{(k+1, i)}^{L}=\frac{t_{i}-t_{k+1}}{t-t_{k+1}} T_{k+1}^{L} \tag{4}\)
\(\varepsilon_{k+1}\)
是从
\(P_{k+1}\)
中抽取的边沿点集,
\(\tilde{\mathcal{E}}_{k+1}\)
是
\(\varepsilon_{k+1}\)
到sweep k+1的开始时间
\(t_{k+1}\)
的重投影;
\(\mathcal{H}_{k+1}\)
是从
\(P_{k+1}\)
中抽取的平面点集,
\(\tilde{\mathcal{H}}_{k+1}\)
是
\(\mathcal{H}_{k+1}\)
到sweep 𝑘k+1的开始时间
\(t_{k+1}\)
的重投影;
推导
\(\varepsilon_{k+1}, \quad \tilde{\varepsilon}_{k+1}, \quad \mathcal{H}_{k+1}, \quad \tilde{\mathcal{H}}_{k+1}\)
之间的对应关系:
\(X_{(k+1, i)}^{L}=R \tilde{X}_{(k+1, i)}^{L}+T_{(k+1, i)}^{L}(1 : 3) \tag{5}\)
上式中,
\(X_{(k+1, i)}^{L}\)
是在
\(\varepsilon_{k+1}\)
或
\(\mathcal{H}_{k+1}\)
中的点𝑖的坐标,同样,
\(\tilde{X}_{(k+1, i)}^{L}\)
对应于
\(\tilde{\varepsilon}_{k+1}\)
和
\(\widetilde{\mathcal{H}}_{k+1}\)
;
\(T_{(k+1, i)}^{L}(1 : 3)\)
是第1维到第3维的
\(T_{(k+1, i)}^{L}\)
内的部分张量元素;
R是由Rodrigues公式得到的旋转矩阵:
\(\boldsymbol{R}=e^{\widehat{\omega} \theta}=\boldsymbol{I}+\widehat{\omega} \sin \theta+\widehat{\omega}^{2}(1-\cos \theta) \tag{6}\)
θ是旋转幅度:
\(\theta=\left\|T_{(k+1, i)}^{L}(4 : 6)\right\| \tag{7}\)
ω是表示旋转方向的单位向量,
\(\omega=T_{(k+1, i)}^{L}(4 : 6) /\left\|T_{(k+1, i)}^{L}(4 : 6)\right\| \tag{8}\)
\(\widehat{\omega}\) 是 \(\omega\) 的斜对称矩阵。
结合以上推导的公式,可以得到
\(\mathcal{E}_{k+1}\)
中的边沿点与对应边沿线之间的关系(距离关系):
\(f_{\mathcal{E}}\left(X_{(k+1, i)}^{L}, T_{k+1}^{L}\right)=d_{\mathcal{E}}, i \in \mathcal{E}_{k+1} \tag{9}\)
同样,我们可以推导得到
\(\mathcal{H}_{k+1}\)
的平面点到对应平面块之间的关系(距离关系):
\(f_{\mathcal{H}}\left(X_{(k+1, i)}^{L}, T_{k+1}^{L}\right)=d_{\mathcal{H}}, i \in \mathcal{H}_{k+1} \tag{10}\)
最后通过Levenberg-Marquardt方法求解雷达运动,将上面两式综合起来,可以得到:
\(\boldsymbol{f}\left(T_{k+1}^{L}\right)=\boldsymbol{d} \tag{11}\)
\(f\)
的每一行都对应一个特征点,对应的
\(d\)
表示相应的距离;
\(f\)
相对于
\(T_{k+1}^{L}\)
求Jacobian矩阵
\(J\)
,
\(J=\partial f / \partial T_{k+1}^{L}\)
通过非线性迭代缩小d值趋近于0来求解上述方程:
\(T_{k+1}^{L} \leftarrow T_{k+1}^{L}-\left(J^{T} J+\lambda \operatorname{diag}\left(J^{T} J\right)\right)^{-1} J^{T} d \tag{12}\)
\(\lambda\) 是通过Levenberg-Marquardt方法确定的比例因子。
D.雷达里程计算法
激光雷达测距算法在算法1中示出。
算法的输入:
上一扫中的点云
\(\overline{P}_{k}\)
,当前扫描中数量正在增加的点云
\(P_{k+1}\)
,上一次递归中得到的位姿变换
\(T_{k+1}^{L}\)
。

算法进行过程:
如果开始新一次的扫描,
\(T_{k+1}^{L}\)
被设置为0(4-6行)。
然后算法从
\(P_{k+1}\)
中抽取特征点来构造
\(\varepsilon_{k+1}\)
和
\(\mathcal{H}_{k+1}\)
(7行)。
对于每个特征点,我们从
\(\overline{P}_{k}\)
中寻找与他们相对应的特征(9-19行)。
运动估计调整后成为稳健拟合方法[27]:算法对每一个特征点分配一个双平方权重(15行)。
特征
\(\mathcal{E}_{k+1}\)
和
\(\mathcal{H}_{k+1}\)
与对应的
\(\overline{P}_{k}\)
中的特征距离大的,分配的权重小;
距离超过一定的门限值,认为是界外点,权值为0。
位姿通过一次迭代进行更新(16行)。
非线性优化在收敛或达到最大迭代次数时停止。
如果算法到了一次sweep的末尾,那么
\(P_{k+1}\)
根据在本次sweep中估计的运动,被投影到时间戳
\(t_{k+2}\)
。否则的话,只返回
\(T_{k+1}^{L}\)
进行下一次的迭代。
算法的输出:
如果是在一次sweep的末尾,返回
\(T_{k+1}^{L}\)
和
\(\overline{P}_{k+1}\)
,
否则返回
\(T_{k+1}^{L}\)
。
6.雷达建图
mapping算法运行频率:比odometry算法运行频率更低,mapping算法每sweep调用一次。
Mapping算法输出:在sweep k+1的末尾,雷达里程计产生一个非失真点云
\(\overline{P}_{k+1}\)
和一个位姿变换
\(T_{k+1}^{L}\)
,
\(T_{k+1}^{L}\)
代表该次sweep在时间
\(\left[t_{k+1}, t_{k+2}\right]\)
的雷达运动。
mapping算法在世界坐标系
\(\{W\}\)
中匹配和注册点云
\(\overline{P}_{k+1}\)
,过程如图8所示。
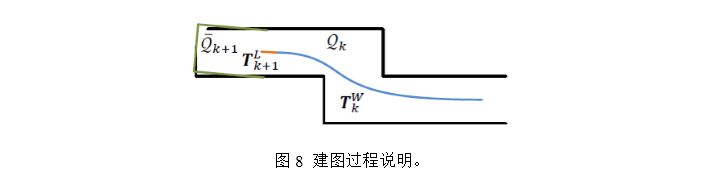
定义以下符号:
\(Q_{k}\)
:地图上累积到sweep k的点云;
\(T_{k}^{W}\)
:在sweep k的末尾,即
\(t_{k+1}\)
时雷达在地图上位姿,以世界坐标系表示;
通过odometry的输出,mapping算法将
\(T_{k}^{W}\)
从
\(t_{k+1}\)
扩展到
\(t_{k+2}\)
,得到
\(T_{k+1}^{W}\)
;
将
\(\overline{P}_{k+1}\)
投影到世界坐标系
\(\{W\}\)
,表示为
\(\overline{Q}_{k+1}\)
。
接下来,算法通过优化雷达位姿 \(T_{k+1}^{W}\) ,将 \(\overline{Q}_{k+1}\) 与 \(Q_{k}\) 𝑄匹配起来。
蓝色曲线代表地图中的雷达位姿 \(T_{k}^{W}\) , \(T_{k}^{W}\) 由mapping算法在sweep k时产生。
橙色曲线代表雷达在sweep k+1时产生的运动 \(T_{k+1}^{L}\) , \(T_{k+1}^{L}\) 由odometry算法计算得到。
通过 \(T_{k}^{W}\) 和 \(T_{k+1}^{L}\) ,由odometry算法发布的非失真点云可以投影到地图中,投影后该地图表示为 \(\overline{Q}_{k+1}\) (图中绿色线段),以前地图中存在的点云表示为 \(Q_{k}\) (黑色线段)。
特征点抽取方式与第5节A的相同,但是用了10倍于它的特征点。
为了寻找特征点的对应关系,将点云存在一个10米的立方体区域地图
\(Q_{k}\)
中。
\(Q_{k}\) 和 \(\overline{Q}_{k+1}\) 相交部分的点云被抽取出来并存储到3D KD-tree中。我们在特征点附近的一定区域内找到 \(Q_{k}\) 中的点。
令S’表示临近点的集合。
对于边缘点:在 S’中,我们只保留在边缘线上的点;
对于平面点,在 S’中,我们只保留在平面片上的点;
然后计算S’的协方差矩阵,记为M,M的特征值和特征向量记为V和E。
如果S’分布在一条边缘线上,那么V中一个特征值就会明显比其他两个大,E中与较大特征值相对应的特征向量代表边缘线的方向。(一大两小,大方向)
如果S’分布在一块平面片上,那么V中一个特征值就会明显比其他两个小,E中与较小特征值相对应的特征向量代表平面片的方向。(一小两大,小方向)
边缘线或平面块的位置通过穿过S’的几何中心来确定。
为计算一个特征点到它对应点之间的距离,我们选择一条边缘上的两个点,和一个平面上的3个点。这样,距离的计算可以用公式(2)和公式(3)来进行。
然后对于每个特征点,我们可以得到一个等式(9)或等式(10)。
但不同的是,
\(\overline{Q}_{k+1}\)
中所有点都有一个相同的时间戳,
\(t_{k+2}\)
。通过Levenberg-Marquardt[26]方法的鲁棒拟合[27]再次解决非线性优化问题。
\(\overline{Q}_{k+1}\)
被注册到地图中。为了均匀地分布点,通过体素网格过滤器缩小地图云,体素大小为5cm立方体。

上图为位姿变换的积分过程。蓝色区域代表雷达建图位姿输出 \(T_{k}^{W}\) , \(T_{k}^{W}\) 每个sweep产生一次。橙色区域是当前sweep内的雷达运动 \(T_{k+1}^{L}\) ,由雷达里程计算法输出。激光雷达的运动估计是两个变换的组合,频率与 \(T_{k+1}^{L}\) 的频率相同。
位姿变换的融合过程:蓝色区域代表雷达建图位姿输出 \(T_{k}^{W}\) , \(T_{k}^{W}\) 每个sweep产生一次。橙色区域代表雷达里程计的位姿变换输出 \(T_{k+1}^{L}\) , \(T_{k+1}^{L}\) 的频率大约为10Hz。相对于地图的激光雷达姿势是两个变换的组合,其频率与激光雷达里程计的相同。
7.实验
A.Indoor & Outdoor Tests
在室内和室外环境都进行了实验,然后和真值进行比较。真值的产生是通过同一个雷达放在多个不同的地方静止扫描,产生的多个点云数据进行ICP匹配之后合成的。然后这个点云和雷达运动时建图的点云进行比较,作为误差。
另外还进行了累积误差的比较,做法是室内时绕某个地方一圈,然后回到原点,地图上开始和结束的两点之间距离就是累积误差。
室外时通过GPS进行了辅助,以GPS信息得到的运动距离和建图的距离比较。
B.Assistance from an IMU
通过IMU数据,对点云预处理的两种方式:
1.通过IMU数据的旋转信息,可以将点云旋转后对齐到到该sweep的初始方向上;
2.通过加速度信息,可以纠正点云的运动失真,让雷达似乎以匀速在运动。
IMU的oritentation通过卡尔曼滤波积分角速率和加速度得到。
实验的三个条件:只用IMU,只用雷达,用IMU+雷达;
实验得到的精度从高到低:IMU+雷达,雷达,IMU。
实验结果证明,IMU在抵消非线性运动时效果明显,这样提出的算法可以处理线性运动。
C.Tests with KITTI Datasets
效果很好,state of art
8.结论和展望
1)本文所提出的算法将整个建图问题分成2个可以并行运行的算法:
1.雷达odometry算法:通过高频率的计算粗略估计速度。
2.雷达mapping算法:进行精确计算以低频产生地图。
两者合起来能够保证精确的运动估计和实时建图。
2)该方法可以利用雷达scan的特征和点云的分布。
3)特征匹配保证odometry算法的快速性,也保证了mapping算法的快速性。
4)本方法的缺陷和未来会改进的地方:
1.当前方法不进行回环检测,将来的工作会将闭环检测加入进去。
2.将当前方法的输出和IMU数据通过kalman滤波器结合,运动估计的漂移。