目录
- 问题描述(Monte Carlo方法)
- 重要性采样(Importance Sampling)
- Sequential Importance Sampling(SIS)
- Resampling:选择一个合适的提议分布
- Basic Particle Filter
- 物理意义
- 粒子滤波器预测的代码示例
- 参考文献
问题描述(Monte Carlo方法)
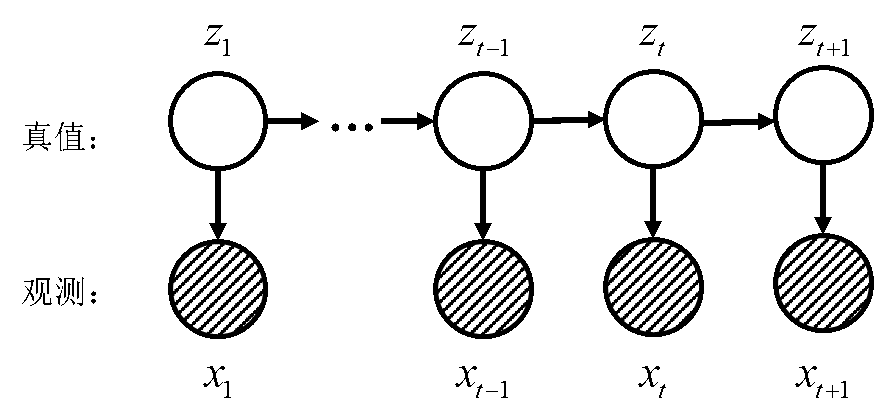
上图中:
1)z表示真值,真值只与前一个状态有关(
\(z_{t}\)
只和
\(z_{t-1}\)
有关,因为假设了马尔科夫性)。
2)x表示了观测,只和对应观测的真值有关。
\(p(z | x)\)
则表示了一个后验概率,这个概率表示我们已经得到了该状态的观测,现在需要知道这个状态的后验概率。
在我们拿到了后验概率之后,对一件事发生的概率我们如果用蒙特卡罗的方法来做,就会对他通过很多次采样的方法,然后取平均来做(求期望)。
我们最终关心的也是它的期望(求取的输出),这个期望是一个概率值,表示了这件事情会发生的概率的大小。即:
\(E_{z | x}[f(z)]=\int f(z) p(z) d z \approx \frac{1}{N} \sum_{i=1}^{N} f\left(z^{i}\right) \tag{1.1}\)
对上面公式的解释:
1)
\(\int f(z) p(z) d z\)
表示的是从
\(p(z)\)
中去采样,当然前提条件是能从
\(p(z)\)
中采样的话;
2)我们用了
\(N\)
个样本,
\(z^{i} \sim p(z), z^{1}, z^{2}, \ldots, z^{N}\)
重要性采样(Importance Sampling)
\(E[f(z)]=\int f(z) p z d z=\int f(z) \frac{p(z)}{q(z)}q(z)dz=\frac{1}{N} \sum_{i=1}^{N} f\left(z^{i}\right) \frac{p\left(z^{i}\right)}{q\left(z^{i}\right)} \tag{1.2}\)
其中:
1)我们在第二个等号处引入一个分布比较简单的
\(q(z)\)
,从
\(q(z)\)
中采样是可行的,这样我们就能从
\(q(z)\)
中采样得到
\(f(z)\)
的后验分布。这里的
\(q(z)\)
叫做提议分布;
2)在第三个等号后,我们令
\(\frac{p\left(z^{i}\right)}{q\left(z^{i}\right)}\)
作为权重;
3)filter的问题最关键的在于求后验概率
\(f\left(z_{t} | x_{1 :t}\right)\)
。
我们令 \(w_{t}^{i}=\frac{p\left(z_{t}^{i} | x_{1 : t}\right)}{q\left(z_{t}^{i} | x_{1 : t}\right)}\) ,有: \(\begin{array}{l}{t=1 : w_{1}^{i}, i=1,2, \ldots, N} \\ {t=2, w_{2}^{i}, i=1,2, \ldots, N}\end{array}\) ,采用了N个样本。
每次求 \(w_{t}^{i}\) 都要求 \(p\left(z_{t}^{i} | x_{1 : t}\right)\) 但这个 \(p\) 很难求,因此我们能否找到一个递推公式,减少计算量呢?这就涉及到SIS的问题了。
Sequential Importance Sampling(SIS)
然后我们想到的就是找到一个
\(w_{t-1}^{i} \rightarrow w_{t}^{i}\)
的递推关系(但其实还有一步归一化需要做)。
我们没有直接求
\(p\left(z_{t} | x_{1: t}\right)\)
的滤波问题(这其实是一个边缘概率),为了避免积分运算,我们先求
\(p\left(z_{1 : t} | x_{1 : t}\right)\)
。
我们需要求的是整个后验,而不是边缘后验,因为我们在t时刻已经知道了前面时刻的状态后验值,所以
\(w_{t}^{i} \propto \frac{p\left(z_{1: t} | x_{1 :t}\right)}{q\left(z_{1: t} | x_{1 :t}\right)}\)
,其中:
\(\begin{array}{1}{p\left(z_{1: t} | x_{1:t}\right)=\frac{p\left(z_{1 : t}, x_{1: t}\right)}{\underbrace{p\left(x_{1 : t}\right)}_{C}}}=\frac{1}{C} p\left(z_{1 : t}, x_{1: t}\right)\\
\begin{array}{l}
{=\frac{1}{C} p\left(x_{t} | z_{1 :t}, x_{1: t-1}\right) p\left(z_{1: t}, x_{1: t-1}\right)} \\
{=\frac{1}{C} p\left(x_{t} | z_{t}\right) p\left(z_{t} | z_{t-1}, x_{1: t-1}\right) p\left(z_{1 :t-1}, x_{1 :t-1}\right)}\\
{=\frac{1}{C} p\left(x_{t} | z_{t}\right) p\left(z_{t} | z_{t-1}\right) p\left(z_{1 :t-1} | x_{1: t-1}\right) \underbrace{p\left(x_{1: t-1}\right)}_{D}}
\\ {=\frac{D}{C} p\left(x_{t} | z_{t}\right) p\left(z_{t} | z_{t-1}\right) p\left(z_{1: t-1} | x_{1: t-1}\right)}
\end{array}
\end{array} \tag{1.3}\)
在公式(1.3)中:
1)因为在时刻t时,前面的观测都是已知的,可以算出来,所以
\(p\left(x_{1 : t}\right)=C\)
是个常数,
\(p\left(x_{1 : t-1}\right)=D\)
也是一个常数;
2)基于观测独立假设,
\(p\left(x_{t} | z_{1 z}, x_{1 z-1}\right)=p\left(x_{t} | z_{t}\right), \quad p\left(z_{t} | z_{1 : t-1}, x_{1 t-1}\right)=p\left(z_{t} | z_{t-1}\right)\)
我们假定有:
\(q\left(z_{1 : t} | x_{1 : t}\right)=q\left(z_{t} | z_{1 : t-1}, x_{1: z}\right) q\left(z_{1 :t-1} | x_{1 : t-1}\right) \tag{1.4}\)
有了上面这个递归式之后,当t=1时,我们能得到 的N个值,当t=2时,我们直接从递推式直接计算得到。
上式(1.5)中,我们还能够进一步简化:
对于这个算法的流程,可以用下面的流程表示:

但是上面这样的算法流程其实会有一个叫做权值退化的问题:
算法运行一定的时间之后,
\(w_{t}^{i}\)
将会变得运来越不平均,某一个原来越大,其余的值越来越小。例如,有100个例子,其中99个粒子权重都是0.001,但是有一个粒子非常接近于1。这时,我们需要通过重采样来解决这个问题。
Resampling:选择一个合适的提议分布
重采样的核心思想其实是一个优胜劣汰的过程,权重低的少播种,权重高的多播种。
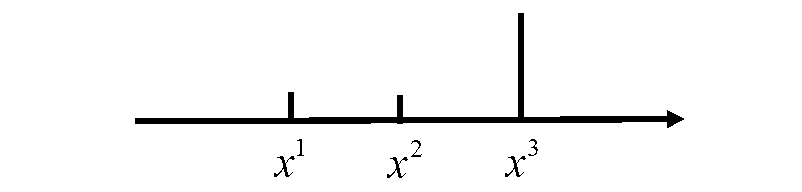
例如对上图进行这样的重采样过程,我们就能得到下图的采样示意:
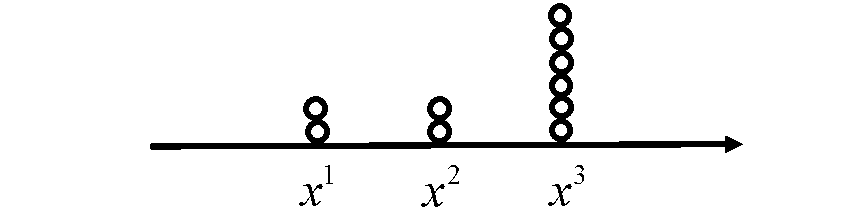
重采样之后每个粒子的权重就相同了。我们用粒子的个数去表达原先的权重,这是最简单的重采样方法。
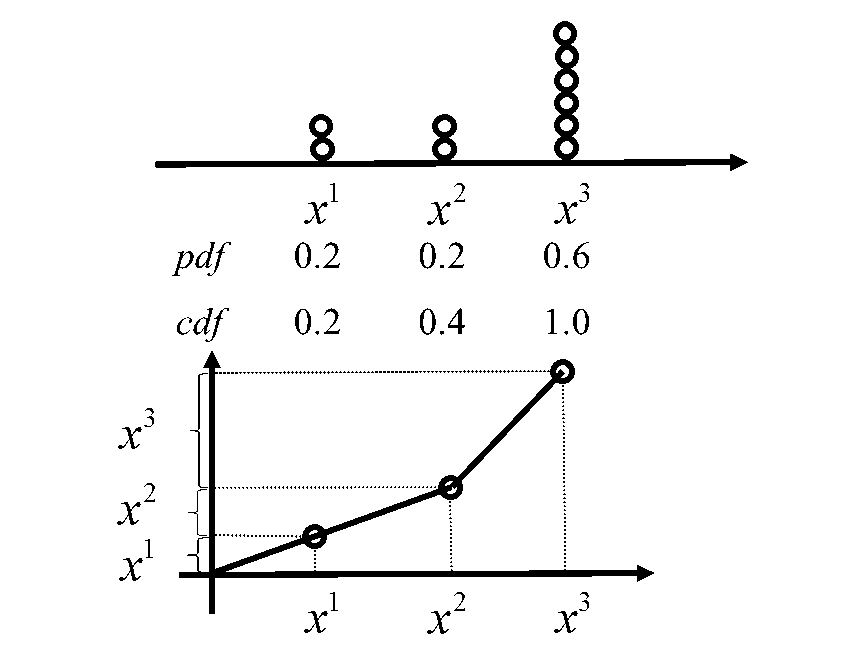 对于上图这样的分布,如果我们从一个
\(u \sim(0,1)\)
的均匀分布,不断取随机数,例如:
对于上图这样的分布,如果我们从一个
\(u \sim(0,1)\)
的均匀分布,不断取随机数,例如:
随机数为0.01时,取
\(x^{1}\)
;
随机数为0.30时,取
\(x^{2}\)
;
随机数为0.60时,取
\(x^{3}\)
;
这样,就实现了上面重采样的想法。
Basic Particle Filter
Basic Particle Filter的主要思想就是SIS+Resampling。
造成权值退化的原因是什么?
维度过高,维度过高要求你的样本空间非常巨大,这时如果用采样的话,我们需要的粒子数目会非常巨大,呈指数级往上增加。
为了解决这个问题,通常有2种办法。第一种办法是重采样(Resampling),第二种办法是选择更合适的提议分布 \(q(z)\) 。
重采样之后,所有的粒子权重都一样,这在上一节已经说明。
对于选择合适的提议分布,令
\(q(z)\)
为状态转移矩阵,即
\(q\left(z_{t} | z_{1 :t-1}, x_{1 : t}\right)=p\left(z_{t} | z_{t-1}\right)\)
这时权重为:
\(w_{i}^{j}=\frac{p\left(x_{i} | z_{t}^{i}\right) p\left(z_{t}^{i} | z_{t-1}^{i}\right)}{q\left(z_{t}^{i} | z_{t-1}^{i}, x_{1 :t}\right)} w_{t-1}^{i}=\frac{p\left(x_{t} | z_{t}^{i}\right) p\left(z_{t}^{i} | z_{t-1}^{i}\right)}{p\left(z_{t}^{i} | z_{t-1}^{i}\right)} w_{t-1}^{i}=p\left(x_{t} | z_{t}^{i}\right) w_{t-1}^{i} \tag{1.7}\)
粒子从哪里来?
\(z_{t}^{i} \sim p\left(z_{t}^{i} | z_{t-1}^{i}\right) \tag{1.8}\)
权重如何确定?
\(w_{t}^{i}=p\left(x_{t} | z_{t}^{i}\right) w_{t-1}^{i} \tag{1.9}\)
上面整个系统就是SIR Filter(Sampling Importance Resampling),其实本质上,它是SIS + Resampling + \(q(z)\) ,这里的 \(q(z)\) 取为 \(p\left(z_{t} | z_{t-1}\right)\) 。
物理意义
对于选择 \(q(z)\) 为 \(p\left(z_{t} | z_{t-1}\right)\) 有什么物理意义?它的直观感受是什么?
这是一个generate and test的过程:
1)首先,从
\(z_{t-1}\)
按照
\(z_{t} \sim p\left(z_{t} | z_{t-1}\right)\)
生成一个
\(z_{t}\)
;
2)然后通过观测的数据,按照公式
\(w_{t}^{i}=p\left(x_{t} | z_{t}^{i}\right) w_{t-1}^{i}\)
得到权重,这个公式的解释就是我观测得到的概率越大,
\(w_{t}^{i}\)
的权重就越高,也就越准确。
粒子滤波器预测的代码示例
%% SIR粒子滤波的应用,算法流程参见博客http://blog.csdn.net/heyijia0327/article/details/40899819
clear all
close all
clc
%% initialize the variables
x = 0.1; % initial actual state
x_N = 1; % 系统过程噪声的协方差 (由于是一维的,这里就是方差)
x_R = 1; % 测量的协方差
T = 75; % 共进行75次
N = 100; % 粒子数,越大效果越好,计算量也越大
%initilize our initial, prior particle distribution as a gaussian around
%the true initial value
V = 2; %初始分布的方差
x_P = []; % 粒子
% 用一个高斯分布随机的产生初始的粒子
for i = 1:N
x_P(i) = x + sqrt(V) * randn;
end
z_out = [x^2 / 20 + sqrt(x_R) * randn]; %实际测量值
x_out = [x]; % the actual output vector for measurement values.
x_est = [x]; % time by time output of the particle filters estimate
x_est_out = [x_est]; % the vector of particle filter estimates.
for t = 1:T
x = 0.5*x + 25*x/(1 + x^2) + 8*cos(1.2*(t-1)) + sqrt(x_N)*randn;
z = x^2/20 + sqrt(x_R)*randn;
for i = 1:N
%从先验p(x(k)|x(k-1))中采样
x_P_update(i) = 0.5*x_P(i) + 25*x_P(i)/(1 + x_P(i)^2) + 8*cos(1.2*(t-1)) + sqrt(x_N)*randn;
%计算采样粒子的值,为后面根据似然去计算权重做铺垫
z_update(i) = x_P_update(i)^2/20;
%对每个粒子计算其权重,这里假设量测噪声是高斯分布。所以 w = p(y|x)对应下面的计算公式
P_w(i) = (1/sqrt(2*pi*x_R)) * exp(-(z - z_update(i))^2/(2*x_R));
end
% 归一化.
P_w = P_w./sum(P_w);
%% Resampling这里没有用博客里之前说的histc函数,不过目的和效果是一样的
for i = 1 : N
x_P(i) = x_P_update(find(rand <= cumsum(P_w),1)); % 粒子权重大的将多得到后代
end % find( ,1) 返回第一个符合前面条件的数的下标
%状态估计,重采样以后,每个粒子的权重都变成了1/N
x_est = mean(x_P);
% Save data in arrays for later plotting
x_out = [x_out x];
z_out = [z_out z];
x_est_out = [x_est_out x_est];
end
t = 0:T;
figure(1);
clf
plot(t, x_out, '--b', t, x_est_out, '-*r','linewidth',2);
set(gca,'FontSize',12); set(gcf,'Color','White');
xlabel('time step'); ylabel('flight position');
legend('True flight position', 'Particle filter estimate');
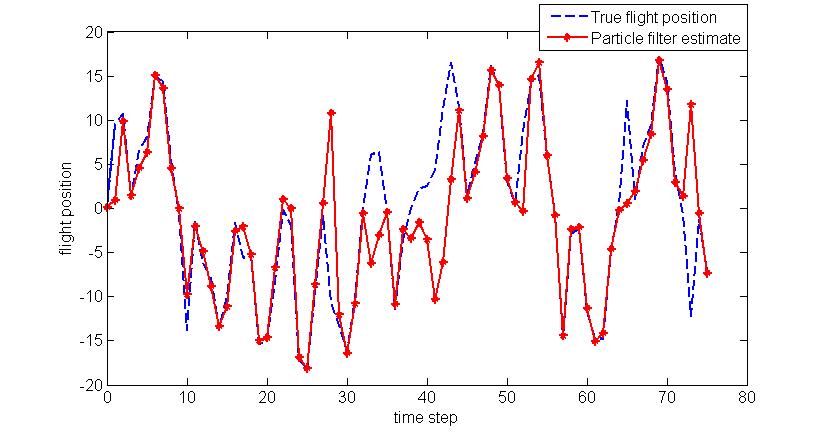
代码运行后的图形为:
参考文献
1.白板推导粒子滤波器
2.Heyijia写的粒子滤波器(经过其他人合并)
3.概率机器人学