目录
- 杨亮《从贝叶斯开始学滤波》中一些问题
- 贝叶斯准则基本理论
- 贝叶斯滤波
- 卡尔曼滤波器
- 扩展卡尔曼滤波器(EKF)
- 迭代扩展卡尔曼滤波器(IEKF)
- sigmapoint卡尔曼滤波器/无迹卡尔曼滤波器(SPKF/UKF)
- 迭代sigmapoint卡尔曼滤波器(ISPKF)
- 粒子滤波器
- 滤波器的分类
- 参考文献
杨亮《从贝叶斯开始学滤波》中一些问题
A Multi-State Constraint Kalman Filter for Vision-aided Inertial Navigation (Anastasios I. Mourikis and Stergios I. Roumeliotis)
这篇文章的主要思想就是用IMU和一个单目相机,单目相机的更新频率没有IMU的频率高。两个数据,要考虑两种数据的时间戳能否对上,在这种情况下,采用融合的方式。一个数据用来预测,另一个数据用来观测,然后用协方差来转换权重。
为什么要讲随机状态和估计?
因为这是一个概率问题。
预测的误差如何累积?
因为我在一个开环的估计里面,不断地走的时候没有人来告诉你走到哪里了,这个误差就会累积。
融合如何进行?
例如图形和加速度不同的信息如何融合?
贝叶斯准则基本理论
贝叶斯准则的基本概念: 两个随机变量 \(X\) 和 \(Y\) 的联合分布由下式给出:
\[p(x,y)=p(X=x,Y=y)\]如果X和Y相互独立,则有
\[p(x,y)=p(x)p(y)\]在已经知道Y=y的基础上,求X的条件概率:
\[p(x|y)=\frac{p(x,y)}{p(y)}\]如果X和Y相互独立:
\[p(x|y)=\frac{p(x,y)}{p(y)}=p(x)\]全概率定理:
\[\begin{align} & p(x|y)=\frac{P(y|x)p(x)}{p(y)}=\frac{p(y|x)p(x)}{\sum\limits_{x'}{p(y|x')p(x')}} \\ & p(x|y)=\frac{p(y|x)p(x)}{p(y)}=\frac{p(y|x)p(x)}{\int{p(y|x')p(x')dx'}} \\ \end{align}\]贝叶斯准则:
\[\begin{align} & p(x|y)=\frac{P(y|x)p(x)}{p(y)}=\frac{p(y|x)p(x)}{\sum\limits_{x'}{p(y|x')p(x')}} \\ & p(x|y)=\frac{p(y|x)p(x)}{p(y)}=\frac{p(y|x)p(x)}{\int{p(y|x')p(x')dx'}} \\ \end{align}\]利用贝叶斯法则,有:
\[p(x|z)=\frac{p(z|x)p(x)}{p(z)}\propto p(z|x)p(x)\]贝叶斯法则左侧通常称为后验概率,右侧 \(p(z|x)\) 称为似然.
另一部分 \(p(x)\) 称为先验。直接求后验分布是困难的,但是求一个状态最优估计,使得在该状态下后验概率最大化(Maxminize a Posterior, MAP),则是可行的:
\[x_{M A P}^{*}=\arg \max p(x | z)=\arg \max p(z | x) p(x)\]贝叶斯法则的分母部分与带估计的状态x无关,因而可以忽略。贝叶斯法则告诉我们,求解最大后验概率相当于最大化似然和先验的乘积。进一步,没有先验时,可以求解x的最大似然估计(Maximize Likehood Estimation,MLE)。
\[x^{*}_{M L E}=\arg \max p(z | x)\]似然:在现在的位姿下,可能产生怎样的观测数据。 因为我们知道观测数据,最大似然可以理解为:在什么样的状态下,最可能产生现在观测到的数据。
贝叶斯滤波
\((\overset{\hat{\ }}{\mathop \cdot }\,)\) 上帽子来表示后验估计
\((\overset{\check{\ }}{\mathop \cdot }\,)\) 下帽子来表示先验估计
\[p\left(x_{k} | \check{x}_{0}, v_{1:k}, y_{0:k}\right)=\eta p\left(y_{k} | x_{k}\right) p\left(x_{k} | \check{x}_{0}, v_{1:k}, y_{0:k-1}\right) \tag{1.1}\]式(1.1)根据全概率公理进行推导,对式(1.1)引入隐藏状态 ,右边部分第二项
\[\begin{array}{l}{p\left(x_{k} | \check{x}_{0}, v_{1:k}, y_{0 : k-1}\right)=\int p\left(x_{k}, x_{k-1} | \check{x}_{0}, v_{1 k}, y_{0 k-1}\right) d x_{k-1}} \\ {=\int p\left(x_{k} | x_{k-1}, \check{x}_{0}, v_{1:k}, y_{0:k-1}\right) p\left(x_{k-1} | \check{x}_{0}, v_{1 : k}, y_{0 : k-1}\right) d x_{k-1}}\end{array} \tag{1.2}\] \[p\left(x_{k} | x_{k-1}, \check{x}_{0}, v_{1: k}, y_{0: k-1}\right)=p\left(x_{k} | x_{k-1}, v_{k}\right) \tag{1.3}\] \[p\left(x_{k-1} | \check{x}_{0}, v_{1 : k}, y_{0 : k-1}\right)=p\left(x_{k-1} | \check{x}_{0}, v_{1 : k-1}, y_{0 : k-1}\right) \tag{1.4}\] \[p\left(x_{k} | \check{x}_{0}, v_{1 : k}, y_{0: k}\right)=\eta p\left(y_{k} | x_{k}\right) \int p\left(x_{k} | x_{k-1}, v_{k}\right) p\left(x_{k-1} | \check{x}_{0}, v_{1 : k-1}, y_{0 : k-1}\right) d x_{k-1} \tag{1.5}\]\(p\left(y_{k} | x_{k}\right)\) 通过 \(g(\centerdot )\) 更新, \(p\left(x_{k} | x_{k-1}, v_{k}\right)\) 利用 \(f(\centerdot )\) 进行预测, \(p\left(x_{k-1} | \check{x}_{0}, v_{1 : k-1}, y_{0 : k-1}\right)\) 是先验置信度。
卡尔曼滤波器
预测的高斯分布:
\[y\left(x, x_{p}, \delta_{p}\right)=\frac{1}{\sqrt{2 \pi \delta_{p}^{2}}} e^{-\frac{\left(x-x_{p}\right)^{2}}{2 \delta_{p}^{2}}}\]观测的高斯分布:
\[y\left(x, x_{m}, \delta_{m}\right)=\frac{1}{\sqrt{2 \pi \delta_{m}^{2}}} e^{-\frac{\left(x-x_{w}\right)^{2}}{2 \delta_{n}^{2}}}\]有观测也有预测:
\[y\left(x, x_{p}, \delta_{p}, x_{m}, \delta_{m}\right)=\frac{1}{2 \pi \sqrt{\delta_{m}^{2} \delta_{p}^{2}}} e^{-\frac{\left(x-x_{p}\right)^{2}}{2 \delta_{p}^{2}}-\frac{\left(x-x_{m}\right)^{2}}{2 \delta_{m}^{2}}}\]假设融合之后的为:
\[y\left(x, x_{f}, \delta_{f}\right)=\frac{1}{\sqrt{2 \pi \delta_{f}^{2}}} e^{-\frac{\left(x-x_{f}\right)^{2}}{2 \delta_{f}^{2}}}\]求解得到
\[\begin{array}{c}{\delta_{f}^{2}=\delta_{p}^{2}-\frac{\delta_{p}^{4}}{\delta_{p}^{2}+\delta_{m}^{2}}} \\ {x_{f}=x_{p}+\frac{\delta_{p}^{2}\left(x_{m}-x_{p}\right)}{\delta_{p}^{2}+\delta_{m}^{2}}}\end{array} \tag{1.6}\]通过上式 (1.6)可以看出, 当 \({\delta_{p}}\) 越大时,说明我的预测值越不准,所以我更应该去相信测量值 \(x_{m}\) ,因此 \(x_{m}\) 的系数越接近于1, \(x_{f}\) 越接近于 \(x_{m}\) 。
当 \({\delta_{p}}\) 越小时,说明我的预测值越准,所以我更应该去相信测量值 \(x_{p}\) ,因此 \(x_{m}\) 的系数越接近于0, \(x_{f}\) 越接近于\(x_{p}\) 。
因为测量值是从观测来的,所以有:
\[Z=H X, \delta_{z}=H \delta_{m}\]根据式(1.6),可以得到卡尔曼增益
\[K=H \delta_{p}^{2} /\left(H^{2} \delta_{p}^{2}+\delta_{m}^{2}\right) \tag{1.7}\]式(1.7)在式(1.6)的增益的基础上有修改,主要是分子上的H。
从上面可以看出,卡尔曼滤波器就是根据高斯模型,简化了在计算时候的一些问题。然后再通过两个量之间的不确定量(方差)来融合估计和观测。
扩展卡尔曼滤波器和SLAM:
- 线性:KF
- 非线性或者部分非线性:EKF
扩展卡尔曼滤波器(EKF)
将置信度和噪声限制为高斯分布,并且对运动模型和观测模型进行线性化,计算贝叶斯滤波中的积分(以及归一化积),得到EKF。 对于一般性的状态模型,定义研究对象的运动和观测模型为,
运动方程: \(x_{k}=f\left(x_{k-1}, v_{k}, w_{k}\right), k=1, \ldots, K \tag{1.8a}\)
观测方程: \(y_{k}=g\left(x_{k}, n_{k}\right), k=0, \ldots, K \tag{1.8b}\)
我们通过线性化将其恢复为加性噪声(取近似)的形式:
\[\begin{aligned} x_{k} &=f\left(x_{k-1}, v_{k}\right)+w_{k} \\ y_{k} &=g\left(x_{k}\right)+n_{k} \end{aligned} \tag{1.9}\]式(1.9)其实是式(1.8)的特殊情况。 由于 \(g(\centerdot )\) 和 \(f(\centerdot )\) 的非线性特性,我们无法计算得到贝叶斯滤波器中的积分的解析解,转而使用线性化的方法,在当前均值(后验状态估计)处展开,对运动和观测模型进行线性化。
\[f\left(x_{k-1}, v_{k}, w_{k}\right) \approx \check{x}_{k}+F_{k-1}\left(x_{k-1}-\check{x}_{k-1}\right)+w_{k}^{\prime} \tag{1.10}\] \[g\left(x_{k}, n_{k}\right) \approx \check{y}_{k}+G_{k-1}\left(x_{k}-\check{x}_{k}\right)+n_{k}^{\prime} \tag{1.11}\]最后推导得到的EKF经典递归方程如下:
预测: \(\begin{aligned} \check{P}_{k} &=F_{k-1} \hat{P}_{k-1} F_{k-1}^{T}+Q_{k}^{\prime} \\ \hat{x}_{k} &=f\left(\check{x}_{k-1}, v_{k}, 0\right) \end{aligned} \tag{1.12}\)
卡尔曼增益: \(\boldsymbol{K}_{k}=\boldsymbol{\check{P}}_{k} \boldsymbol{G}_{k}^{T}\left(\boldsymbol{G}_{k} \boldsymbol{\check{P}}_{k} \boldsymbol{G}_{k}^{T}+\boldsymbol{R}_{k}^{\prime}\right)^{-1} \tag{1.13}\)
更新: \(\begin{aligned} \hat{P}_{k} &=\left(1-K_{k} G_{k}\right) \check{P}_{k} \\ \hat{x}_{k} &=\check{x}_{k}+K_{k}\left(y_{k}-g\left(\check{x}_{k}, 0\right)\right) \end{aligned} \tag{1.14}\)
对以上公式的说明:
\[F_{k-1}=\left.\frac{\partial f\left(x_{k-1}, v_{k}, w_{k}\right)}{\partial x_{k-1}}\right|_{\hat{x}_{k-1}, v_{k}, 0} \tag{1.15}\] \[\begin{array}{l}{Q_{k}^{\prime} : p\left(x_{k} | x_{k-1}, v_{k}\right) \approx N\left(\check{x}_{k}+F_{k-1}\left(x_{k-1}-\hat{x}_{k-1}\right), Q_{k}^{\prime}\right)} \\ {Q_{k}^{\prime}=E\left[w_{k}^{\prime} w_{k}^{\prime T}\right] \approx E\left[\left(x_{k}-E\left[x_{k}\right]\right)\left(x_{k}-E\left[x_{k}\right]\right)^{T}\right]}\end{array} \tag{1.16}\] \[G_{k}=\left.\frac{\partial g\left(x_{k}, n_{k}\right)}{\partial x_{k}}\right|_{\check{x}_{k}, 0} \tag{1.17}\] \[\boldsymbol{R}_{k}^{\prime}=E\left[\boldsymbol{n}_{k}^{\prime} \boldsymbol{n}_{k}^{\prime T}\right] \approx E\left[\left(y_{k}-E\left[y_{k}\right]\right)\left(y_{k}-E\left[y_{k}\right]\right)^{T}\right] \tag{1.18}\]EKF的主要问题在于,其线性化的工作点是估计状态的均值,而不是真实状态。这可能导致EKF在某些情况下快速地发散。
迭代扩展卡尔曼滤波器(IEKF)
对非线性观测模型
\[y_{k}=g\left(x_{k}, n_{k}\right) \tag{1.19}\]选取一个点 \(x_{o p, k}\) 进行线性化,得到:
\[\begin{array}{l}{g\left(x_{k}, n_{k}\right) \approx y_{o p, k}+G_{k}\left(x_{k}-x_{o p, k}\right)+n_{k}^{\prime}} \\ {y_{o p, k}=g\left(x_{o p, k}, 0\right), G_{k}=\left.\frac{\partial g\left(x_{k}, n_{k}\right)}{\partial x_{k}}\right|_{x_{op, k}, 0}, n_{k}^{\prime}=n_{k} \frac{\partial g\left(x_{k}, n_{k}\right)}{\partial n_{k}} | _{x_{op, k}, 0}}\end{array} \tag{1.20}\]将时刻为k处的状态和测量的两盒概率近似为高斯分布:
\[\begin{array}{1}{ p\left(\boldsymbol{x}_{k}, \boldsymbol{y}_{k} | \boldsymbol{\check{x}}_{0}, \boldsymbol{v}_{1 : k}, \boldsymbol{y}_{0 : k-1}\right) \approx \boldsymbol{N}\left( \left[ \begin{array}{c}{\mu_{x,k}} \\ \mu_{y,k}\end{array}\right],\left[ \begin{array}{ll}{\Sigma_{x x, k}} & {\Sigma_{x y, k}} \\ {\Sigma_{y x, k}} & {\Sigma_{y y, k}}\end{array}\right]\right)} \\{= N \left( \left[ \begin{array}{c}{\check{x}_{k}} \\ {y_{o p, k}+G_{k}\left(\check{x}_{k}-x_{op, k}\right)}\end{array}\right] , \left[ \begin{array}{ll}{\check{P}_{k}} & {\check{P}_{k}G_{k}^{T}}\\{G_{k}\check{P}_{k}^{T}} &{G_{k} \check{P}_{k} G_{k}^{T}+R_{k}^{\prime} } \end{array} \right] \right)} \end{array} \tag{1.21}\]然后结合广义高斯滤波的校正方程,得到IEKF的公式:
\[\begin{aligned} \boldsymbol{K}_{k} &=\boldsymbol{\check{P}}_{k} \boldsymbol{G}_{k}^{T}\left(\boldsymbol{G}_{k} \boldsymbol{\check{P}}_{k} \boldsymbol{G}_{k}^{T}+\boldsymbol{R}_{k}^{\prime}\right)^{-1} \\ \boldsymbol{\hat{P}}_{k} &=\left(1-\boldsymbol{K}_{k} \boldsymbol{G}_{k}\right) \boldsymbol{\check{P}}_{k} \\ \hat{\boldsymbol{x}}_{k} &=\boldsymbol{\check{x}}_{k}+\boldsymbol{K}_{k}\left(\boldsymbol{y}_{k}-\boldsymbol{y}_{o p, k}-\boldsymbol{G}_{k}\left(\boldsymbol{\check{x}}_{k}-\boldsymbol{x}_{o p, k}\right)\right) \end{aligned} \tag{1.22}\]IEKF与EKF的公式的唯一区别在于线性化的工作点,如果我们让线性化的工作点为预测先验的均值,即 \(\boldsymbol{x}_{o p, k}=\boldsymbol{\check{x}}_{k}\) ,那么IEKF就和EKF完全相同。
但是,如果我们让每次迭代中的工作点设置为上一次迭代的后验均值,将得到更好的结果。
\[\boldsymbol{x}_{\boldsymbol{op}, k} \leftarrow \hat{\boldsymbol{x}}_{k} \tag{1.23}\]只有在第一次迭代时,令 \(\boldsymbol{x}_{\boldsymbol{op}, k} \leftarrow \check{\boldsymbol{x}}_{k} \tag{1.23}\) ,其他情况都参照公式(1.23),进行迭代。
sigmapoint卡尔曼滤波器/无迹卡尔曼滤波器(SPKF/UKF)
将概率分布函数传入非线性函数的方法大概有3种:蒙特卡罗方法,线性化方法以及sigmapoint方法。
1.蒙特卡罗方法
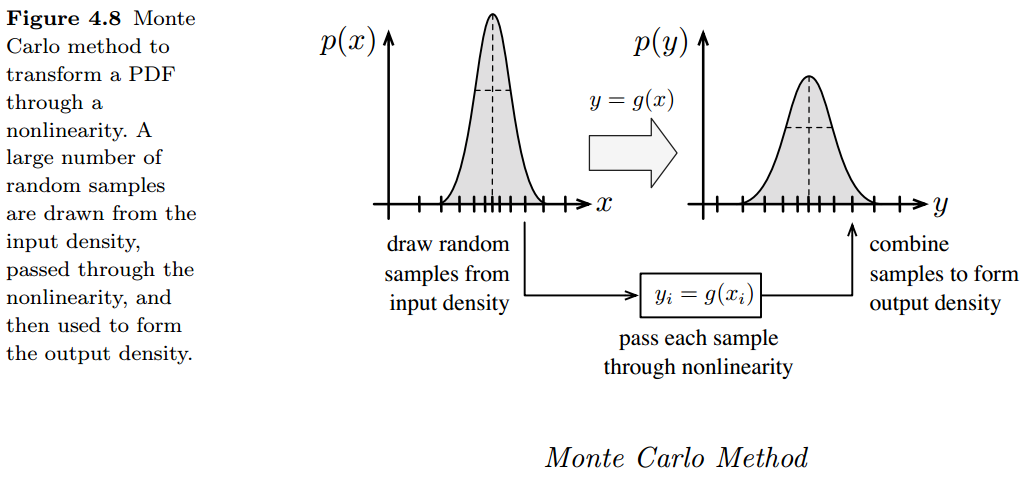
2.线性化方法

3.sigmapoint方法
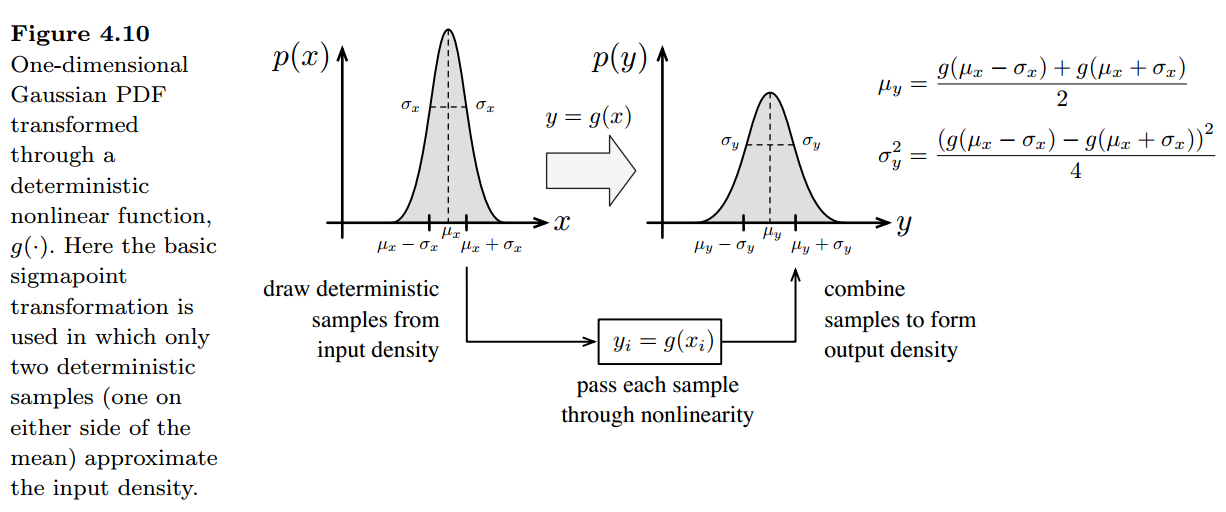
在非线性的运动和观测模型中,不采用线性化的方法,而是使用sigmapoint变换来传递概率分布函数。这样就导出了sigmapoint卡尔曼滤波器(SPKF),也称为无迹卡尔曼滤波(UKF)。
SPKF分为2个部分,第一部分为预测步骤,第二部分是校正步骤。
预测:
预测步骤主要内容是将先验置信度 \(\left\{\hat{x}_{k-1}, \hat{P}_{k-1}\right\}\) 转换为预测置信度 \(\left\{\hat{x}_{k}, \hat{P}_{k}\right\}\)
1.先验置信度和运动噪声都有不确定性,将他们按以下方式堆叠在一起:
\[\mu_{z}=\left[ \begin{array}{c}{\hat{x}_{k-1}} \\ {0}\end{array}\right], \Sigma_{z z}=\left[ \begin{array}{cc}{\hat{P}_{k-1}} & {0} \\ {0} & {Q_{k}}\end{array}\right] \tag{1.24}\] \[L=\operatorname{dim}\left(\mu_{z}\right) \tag{1.25}\]2.将 \(\left\{\boldsymbol{\mu}_{z}, \Sigma_{zz}\right\}\) 转化为sigmapoint表示:
\[\begin{array}{l}{L L^{T}=\Sigma_{z z}} \\ {z_{0}=\mu_{z}} \\ {z_{i}=\mu_{z}+\sqrt{L+k}col_{i} L} \\ {z_{i+L}=\mu_{z}-\sqrt{L+k}{col}_{i} L, i=1, \ldots, L}\end{array} \tag{1.26}\]3.对每个sigmapoint展开为状态和运动噪声的形式
\[\boldsymbol{z}_{i}=\left[ \begin{array}{c}{\boldsymbol{\hat{x}}_{k-1, i}} \\ {\boldsymbol{w}_{k, i}}\end{array}\right] \tag{1.27}\]将每个sigmapoint代入非线性运动模型进行精确求解
\[\hat{x}_{k, i}=f\left(\hat{x}_{k-1, i}, v_{k}, w_{k, i}\right), i=0, \dots, 2 L \tag{1.28}\]4.将转换后的sigmapoint重新组合成预测置信度:
\[\begin{aligned} \check{x}_{k} &=\sum_{i=0}^{2 L} \alpha_{1} \check{x}_{k, i} \\ \check{P}_{k} &=\sum_{i=0}^{2 I} \alpha_{i}\left(\check{x}_{k, i}-\check{x}_{k}\right)\left(\check{x}_{k, i}-\check{x}_{k}\right)^{T} \\ \alpha_{i} &=\left\{\begin{array}{l}{\frac{k}{L+k}, i=0} \\ {\frac{1}{2} \frac{1}{L+k}}, others\end{array}\right. \end{aligned} \tag{1.29}\]校正:
后验概率是 \(p \sim N\left(\hat{x}_{k}, \hat{P}_{k}\right)\)
校正步骤主要是一次求解 \(\boldsymbol{K}_{k}, \boldsymbol{\hat{P}}_{k}, \boldsymbol{\hat{x}}_{k}\) 。使用SP变换得到更优的 \(\boldsymbol{\mu}_{y, k}, \Sigma_{y y, k}, \Sigma_{x y, k}\) ,然后代入到求解 \(\boldsymbol{K}_{k}, \boldsymbol{\hat{P}}_{k}, \boldsymbol{\hat{x}}_{k}\) 的公式中去,进而得到后验值。采用下面的步骤:
1.预测置信度和观测噪声堆叠在一起:
\[\mu_{z}=\left[ \begin{array} \\ {\check{x}_{k}} \\ {0}\end{array}\right], \Sigma_{z}=\left[ \begin{array}{cc}{\check{P}_k} & {0} \\ {0} & {R_{k}}\end{array}\right] \tag{1.30}\] \[L=\operatorname{dim}\left(\boldsymbol{\mu}_{z}\right) \tag{1.31}\]2.将 \(\left\{\boldsymbol{\mu}_{z}, \Sigma_{z z}\right\}\) 转化为sigmapoint表示:
\[\begin{array}{l}{L L^{T}=\Sigma_{z z}} \\ {z_{0}=\mu_{z}} \\ {z_{i}=\mu_{z}+\sqrt{L+k} col _{i} L} \\ {z_{i+L}=\mu_{z}-\sqrt{L+k} col _{i} L, i=1 \ldots, L}\end{array} \tag{1.32}\]3.对每个sigmapoint展开为状态和运动噪声的形式
\[z_{i}=\left[ \begin{array} \\ {\check{x}_{k, i}} \\ {n_{k, i}}\end{array}\right] \tag{1.33}\]将每个sigmapoint代入非线性运动模型进行精确求解
\[\check{y}_{k i}=f\left(\check{x}_{k_{k} i}, n_{k i}\right), i=0, \ldots, 2 L \tag{1.34}\]4.将转换后的sigmapoint重新组合得到最终的结果:
\[\begin{aligned} \mu_{y, k} &=\sum_{i=0}^{2 L} \alpha_{i} \check{y}_{k, i} \\ \Sigma_{y, k} &=\sum_{i=0}^{2 L} \alpha_{i}\left(\check{y}_{k, i}-\mu_{y, k}\right)\left(\check{y}_{k, i}-\mu_{j, k}\right)^{T} \\ \Sigma_{x y, k} &=\sum_{i=0}^{2 L} \alpha_{i}\left(\check{x}_{k, i}-x_{k}\right)\left(\check{y}_{k, i}-\mu_{y, k}\right)^{T} \\ \alpha_{i}&=\left\{\begin{array}{l}{\frac{k}{L+k}, i=0} \\ {\frac{1}{2} \frac{1}{L+k},others}\end{array}\right. \end{aligned} \tag{1.35}\]SPKF的优点:1)不需要任何解析形式的导数 2)仅使用了基本的线性代数运算,不需要非线性运动和观测模型的封闭形式(解析解)。
迭代sigmapoint卡尔曼滤波器(ISPKF)
ISPKF比单次的版本更优秀。在每次迭代中,我们在工作点 \(x_{op,k}\) 附近计算作为输入的sigmapoint。第一次迭代时,令 \(x_{op,k}=\check{x}_{k}\) ,但在之后每次迭代中 都会被优化。 1.预测置信度和观测噪声都有不确定性,将他们按以下方式堆叠:
\[\boldsymbol{\mu}_{z}=\left[ \begin{array}{c}{\boldsymbol{x}_{o p, k}} \\ {0}\end{array}\right], \Sigma_{z z}=\left[ \begin{array}{cc}{\check{P}_{k}} & {0} \\ {0} & {\boldsymbol{R}_{k}}\end{array}\right] \tag{1.36}\] \[L=\operatorname{dim}\left(\boldsymbol{\mu}_{z}\right) \tag{1.37}\]2.将 \(\left\{\mu_{z}, \Sigma_{zz}\right\}\) 转化为sigmapoint表示:
\[\begin{array}{l}{L L^{T}=\Sigma_{z z}} \\ {z_{0}=\mu_{z}} \\ {z_{i}=\mu_{z}+\sqrt{L+k} \operatorname{col}_{i} L} \\ {z_{i+L}=\mu_{z}-\sqrt{L+k} \operatorname{col}_{i} L, i=1, \ldots, L}\end{array} \tag{1.38}\]3.对每个sigmapoint展开为状态和观测噪声形式并代入非线性观测模型求解
\[\boldsymbol{z}_{i}=\left[ \begin{array}{c}{\boldsymbol{x}_{o p, k, i}} \\ {\boldsymbol{n}_{k, i}}\end{array}\right] \tag{1.39}\] \[y_{o p_{, k, i}}=g\left(x_{o_{o p, k, i}}, n_{k, i}\right), i=0, \ldots, 2 L \tag{1.40}\]4.将转换后的sigmapoint重新组合得到最终的结果:
\[\begin{aligned} \mu_{y, k} &=\sum_{i=0}^{2 L} \alpha_{i} {y}_{op,k, i} \\ \Sigma_{y y, k} & =\sum_{i=0}^{2 L} \alpha_{i}\left(y_{o p, k, i}-\mu_{y, k}\right)\left(y_{o p, k, i}-\mu_{y, k}\right)^{T} \\ \Sigma_{x y, k} &=\sum_{i=0}^{2 L} \alpha_{i}\left(x_{op, k, i}-x_{o p, k}\right)\left(y_{op, k, i}-\mu_{y, k}\right)^{T} \\ \Sigma_{x x, k} & =\sum_{i=0}^{2 L} \alpha_{i}\left(x_{o p, k, i}-x_{o p, k}\right)\left(x_{o p, k, i}-x_{o p, k}\right)^{T} \\ \alpha_{i}&=\left\{\begin{array}{l}{\frac{k}{L+k}, i=0} \\ {\frac{1}{2} \frac{1}{L+k},others}\end{array}\right. \end{aligned} \tag {1.41}\]然后求得
\[\begin{aligned} K_{k} &=\Sigma_{x y, k} \Sigma_{y y, k}^{-1} \\ P_{k} &=\Sigma_{x x, k}-K_{k} \Sigma_{y x, k} \\ x_{k} &=x_{k}+K_{k}\left(y_{k}-\mu_{y, k}-\Sigma_{y x, k} \Sigma_{x x, k}^{-1}\left(x_{k}-x_{o p, k}\right)\right) \end{aligned} \tag{1.42}\]最初我们将工作点设置为先验的均值, \(x_{op,k}=\check{x}_{k}\) ,在随后的迭代中我们将其设置为当前迭代的最优估计: \(x_{op,k}=\hat{x}_{k}\) ,当下一次迭代量足够小时,该过程停止。
IEKF对应于EKF。
ISPKF对应于SPKF,令 \(x_{op,k}=\check{x}_{k}\) ,同样有
\[\hat{x}_{k}=\check{x}_{k}+K_{k}\left( y_{k}- \mu_{y,k} \right) \tag{1.43}\]粒子滤波器
粒子滤波器降低了卡尔曼滤波器的状态矩阵,但是对于单个的计算单元增加了计算量。
滤波器的分类
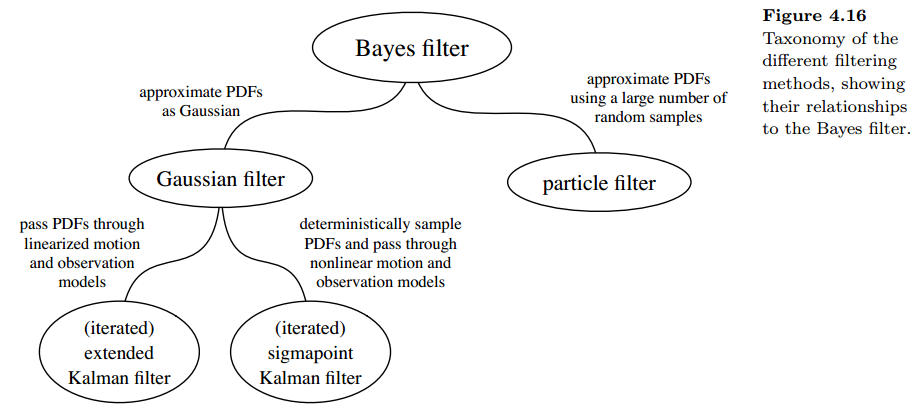
上面的分类主要是根据将概率分布函数传入非线性函数的方法来分类的。线性化方法和sigmapoint方法是假设概率分布函数为高斯的来进行的。
参考文献
[1] 概率机器人学
[2] 机器人学中的状态估计