LeGO-LOAM是一种在LOAM之上进行改进的激光雷达建图方法,建图效果比LOAM要好,但是建图较为稀疏,计算量也更小了。
本文原地址:wykxwyc的博客
github注释后LeGO-LOAM源码:LeGO-LOAM_NOTED 关于代码的详细理解,建议阅读:
1.地图优化代码理解
3.特征关联代码理解
以上博客会随时更新,如果对你有帮助,请点击注释代码的github仓库右上角star按钮,你的鼓励将给我更多动力。
目录
摘要
LeGO-LOAM特点
1)一种轻量级的,可在嵌入式平台上运行
2)点云分割去除噪声
3)带有地面优化的实时6自由度估计(在分割和优化步骤中利用了地平面的存在)
4)回环检测
LeGO-LOAM过程:
1)首先应用点云分割滤除噪声
2)然后特征抽取接收特征平面和特征边
3)两步Levenberg-Marquardt优化方法:地面提取的平面特征用于在第一步中获得
\(\left[t_{z}, \theta_{roll}, \theta_{pitch}\right]\)
,在第二步中,通过匹配从分段点云提取的边缘特征来获得其余部分的变换
\(\left[t_{x}, t_{y}, \theta_{yaw}\right]\)
相比于LOAM,LeGO-LOAM实现了类似或更好的精度,同时降低了计算开销。
1.简介
基于视觉的方法在闭环检测方面有很多优势,但基于视觉对于照明和观测点敏感度高,容易不稳定。 雷达对于光照不敏感。
关于ICP:
最典型的寻找两个雷达scans之间的坐标变换的方法是iterative closest point(ICP)。通过逐点找到对应,ICP迭代地对齐两组点,直到满足停止标准。当扫描包括大量点时,ICP可能遭受过高的计算成本。
学术界已经提出了许多ICP的变体来提高其效率和准确性[2]。
[3] 介绍了一种点到平面的ICP变体,它将点与局部平面贴片相匹配。
Generalized-ICP [4]提出了一种匹配两次扫描的局部平面贴片的方法。
此外,一些ICP变体利用并行计算来提高效率[5]-[8]。
基于特征的匹配方法通过从环境中提取代表性特征而需要较少的计算资源。
成为特征的条件:1)有效匹配2)视点无关。
点特征直方图(PFH)[9] 和视角特征直方图(VFH)[10],使用简单有效的技术从点云中提取这些特征的方法。
[11]中介绍了使用Kanade-Tomasi角点检测器从点云中提取通用特征的方法。
[12]中讨论了从密集点云中提取线和平面特征的框架。
对点云使用特征注册的算法:
[13]和[14]提出了一种关键点选择算法:在本地集群中执行点曲率计算,然后使用所选关键点来执行匹配和位置识别。
[15]通过将点云投影到距离图像上并分析深度值的二阶导数,然后从具有大曲率的点中选择特征以进行匹配和位置识别。
[16]中提出了基于平面的配准算法。室外环境(例如森林)可能限制这种方法的应用。
[17]的领口线段(CLS)方法,专为Velodyne激光雷达设计。CLS使用来自扫描的两个连续“环”的点随机生成线。然后生成两个线云并用于注册。但random generation of lines 对该方法有干扰。
[18]中提出了基于分割的配准算法。SegMatch首先将分段应用于点云。然后基于其特征值和形状直方图为每个片段计算特征向量。随机森林用于匹配来自两次扫描的片段。虽然这种方法可以用于在线姿态估计,但它只能提供大约1Hz的定位更新。
[19]和[20]提出了LOAM。LOAM对边缘/平面扫描匹配执行点特征以找到扫描之间的对应关系。通过计算其局部区域中的点的粗糙度来提取特征。选择具有高粗糙度值的点作为边缘特征。类似地,具有低粗糙度值的点被指定为平面特征。通过在两个单独的算法之间高明地划分估计问题来实现实时性能。一种算法以高频率运行并以低精度估计传感器速度。 另一种算法以低频运行但返回高精度运动估计。将两个估计值融合在一起以产生高频率和高精度的单个运动估计。LOAM的最终精确度是KITTI测距基准站点[21]上仅激光雷达估算方法所能达到的最佳效果。
LeGO-LOAM的适用场景:
1)没有强大的计算单元(工控机)。
2)由于尺寸有限,许多无人驾驶地面车辆(UGV)没有悬架,小型UGV经常遇到非平滑运动,所获取的数据经常失真,在两次连续扫描之间也很难找到可靠的特征对应关系。
在上述条件中,当资源有限时,LOAM的性能会恶化。恶化原因如下:
1)由于需要计算密集3D点云中每个点的粗糙度,因此轻量级嵌入式系统上的特征提取更新频率无法始终跟上传感器更新频率。
2)数据失真,嘈杂环境中操作UGV也对LOAM提出了挑战。由于激光雷达的安装位置通常在小UGV上接近地面,因此来自地面的传感器噪声可能是恒定的存在。例如,草的距离信息可能导致高粗糙度值。因此,需要从这些点抽取掉不可靠的边缘特征。类似地,也可以从树叶返回的点提取边缘或平面特征。这些特征对于扫描匹配通常是不可靠的,因为在两次连续扫描中可能看不到相同的草叶或叶片。使用这些功能可能会导致注册不准确和大漂移。
基于上面的原因,提出 LeGO-LOAM,用于复杂环境中对UGV进行姿态估计。优点:
1)LeGO-LOAM是轻量级的,因为可以在嵌入式系统上实现实时姿态估计和建图。
2)去除失真数据,在地面分离之后,执行点云分割以丢弃可能表示不可靠特征的点。
3)LeGO-LOAM引入地面优化,因为我们引入了两步优化姿势估计。从地面提取的平面特征用于在第一步中获得
\(\left[t_{z}, \theta_{roll}, \theta_{pitch}\right]\)
。在第二步中,通过匹配从分段点云提取的边缘特征来获得其余部分的变换\(\left[t_{x}, t_{y}, \theta_{yaw}\right]\)
。
4)集成了回环检测以校正运动估计漂移的能力。
本文的其余部分安排如下:
第2节介绍了用于实验的硬件。
第3节详细描述了所提出的方法。
第4部分介绍了各种户外环境的一系列实验。
2.系统硬件
VLP-16测量范围高达100米,精度为±3厘米。它具有30°(15°)的垂直视场(FOV)和360°的水平FOV。16通道传感器提供2°的垂直角分辨率。水平角分辨根据旋转速率不同,从0.1°到0.4°变化。在整篇论文中,我们选择10Hz的扫描速率,其提供0.2°的水平角分辨率。
HDL-64E(通过KITTI数据集研究这项工作中)也具有360°的水平FOV,但是它还有48个通道。 HDL-64E的垂直FOV为26.9°。
本文中使用的UGV是Clearpath Jackal。 由270瓦时的锂电池供电,最大速度为2.0米/秒,最大有效载荷为20千克。Jackal还配备了低成本惯性测量单元(IMU),CH Robotics UM6方向传感器。
提出的框架在Nvidia Jetson TX2和2.5GHz i7-4710MQ的laptop上验证:
Jetson TX2是一款嵌入式计算设备,配备ARM Cortex-A57 CPU。
笔记本电脑CPU以匹配[19]和[20]中使用的计算硬件,和Zhang Ji论文中的配置相同。
3.轻量级激光雷达测量和建图
A.系统概述
框架概述如图1所示。
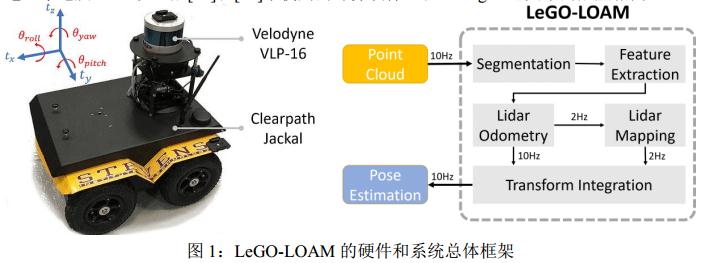
系统输入:接收来自3D激光雷达的输入。
输出:6 DOF姿势估计。
整个系统分为五个模块:
1)分割,采用单个扫描的点云,并将其投影到距离图像上进行分割。分割后的点云然后被发送到2)特征提取模块。
3)雷达里程计使用从前一模块中提取的特征来找到与连续扫描相关的变换。
特征在4)雷达建图模块中进一步处理,雷达建图将它们注册到全局点云图。
5)变换融合模块融合了激光雷达里程计和激光雷达建图的姿态估计结果,并输出最终的姿态估计。
与[19]和[20]的原始LOAM框架相比,所提出的系统寻求提高地面车辆的效率和准确性。
B.分割
点云 \(P_{t}=\left\{p_{1}, p_{2}, \dots, p_{n}\right\}\) 为在时间t时获得的点云, \(p_{i}\) 代表的是 \(p_{t}\) 中的一个点。 \(r_{i}\) 表示从对应点 \(p_{i}\) 到传感器的欧几里德距离。
\(P_{t}\) 首先投影到range image上:
VLP-16分辨率:水平0.2°,垂直2°,投影距离图像分辨率:1800×16(360/0.2×16)。 每个 \(p_{i}\) 现在由range image中的像素表示。
地平面估计[22]:
在分割之前进行地面图像的逐列评估,其可以被视为,用于地面点提取。在此过程之后,可能代表地面的点被标记为地面点而不用于分割。
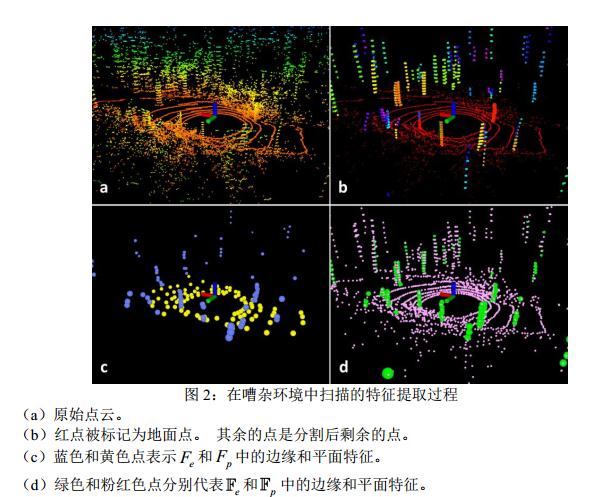
对点云进行分组聚类,仅保留可表示大对象(例如树干)和地面点的点(图2(b)):
1)来自同一群集的点将分配唯一标签。 地面点是一种特殊类型的群集。将分段应用于点云可以提高处理效率和特征提取精度。
2)环境噪声多,树叶这些特征不可靠,同时为提高速度,我们省略少于30个点的聚类,
每个点获得三个属性:
1)其标签作为基点或分段点,
2)其在距离图像中的列和行索引
3)其range value。
C.特征提取
特征提取过程类似于Zhang Ji的论文[20],但不从原始点云提取,而是从地面点和segmented points提取特征。
1)计算每个点
\(p_{i}\)
粗糙度:
\(c=\frac{1}{|S| \cdot\left\|r_{i}\right\|}\left\|\sum_{j \in S, j \neq i}\left(r_{j}-r_{i}\right)\right\|\)
令S作为range image中同一行的连续点
\(p_{i}\)
的点集。S中有一半的点位于
\(p_{i}\)
的两侧。本文中
\(|S|=10\)
。
2)为了从所有方向均匀地提取特征,将range image水平划分为几个相等的sub-image。
3)按每个点的粗糙度值 对sub-image的每一行中的点进行排序。
4)我们使用阈值
\(c_{th}\)
来区分不同类型的特征。
\(c>c_{th}\)
:边特征,
\(c<c_{th}\)
:平面特征。
5)从sub-image的每一行中选取不属于地面,且有最大c值的
\(n_{\mathbb{F}_{e}}\)
个特征边。
6)选取最小c的
\(n_{\mathbb{F}_{p}}\)
个平面特征点(可以标记为地面或分段点)
7)
\(\mathbb{F}_{e}\)
和
\(\mathbb{F}_{p}\)
和 为所有sub-image的边缘和平面特征集合。如图2(d)。
8)从子图中的每一行提取具有最大c的
\(n_{F_{e}}\)
个边缘特征,他们不属于地面。
9)从子图中的每一行提取具有最小c的
\(n_{F_{p}}\)
个平面特征,该特征点必须是地面点。
10)前两步产生边缘集合
\(F_{e}\)
,平面集合
\(F_{p}\)
。
\(F_{e} \subset \mathbb{F}_{e}, F_{p} \subset \mathbb{F}_{p}\)
,
\(F_{e}\)
和
\(F_{p}\)
的特征如图2(c)。
上面对特征点和特征平面各进行了2次抽取。将360°范围图像分为6个子图像。每个子图像的分辨率为300乘16。令 \(n_{F_{e}}=2,n_{F_{p}}=4,n_{\mathbb{F}_{e}}=40,n_{\mathbb{F_{p}}}=80\) 。
D.雷达里程计
估计两次连续扫描之间的传感器运动:
通过点对边和点对面扫描匹配找到两次扫描之间的变换。从前一次扫描的特征集合 \(\mathbb{F_{e}^{t-1}}\) 和 \(\mathbb{F_{p}^{t-1}}\) 中找到 \(n_{F_{p}}\) 和 \(n_{F_{e}}\) 中点的相应特征。
改进以提高匹配的准确性和效率:
1)标签匹配:
\(F_{e}^{t}\) 和 \(F_{p}^{t}\) 中的特征都用标签进行编码,因此从 \(\mathbb{F_{e}^{t-1}}\) 和 \(\mathbb{F_{p}^{t-1}}\) 寻找具有相同标签的对应点。
对于 \(F_{p}^{t}\) 中的平面点,只有在 \(\mathbb{F_{p}^{t-1}}\) 中被标记为地面点的才会被用于寻找 \(F_{p}^{t}\) 中对应的平面片。
对于 \(F_{e}^{t}\) 中的边缘特征,从 \(\mathbb{F_{e}^{t-1}}\) 中寻找对应的边缘线。
这种方式提高匹配准确性,缩小了潜在对应特征的数量。
2)两步L-M优化:
两步L-M优化方法,最佳转换T分两步找到:
1)将 \(F_{p}^{t}\) 中的平面点和 \(\mathbb{F_{p}^{t-1}}\) 中对应的特征相匹配,估计得到 \(\left[t_{z}, \theta_{r o l l}, \theta_{p i t c h}\right]\)
2)将 \(F_{e}^{t}\) 中的边缘点和 \(\mathbb{F_{e}^{t-1}}\) 中对应的特征相匹配,加上附加条件 \(\left[t_{z}, \theta_{roll}, \theta_{pitch}\right]\) ,得到剩下的 \(\left[t_{x}, t_{y}, \theta_{y a w}\right]\) 。
虽然 \(\left[t_{x}, t_{y}, \theta_{y a w}\right]\) 也可以放在第一步时进行,但这样准确度不高,得到的结果也不能继续放在第二步中使用。
2个连续scan之间的6自由度变换通过融合 \(\left[t_{z}, \theta_{roll}, \theta_{pitch}\right]\) 和 \(\left[t_{x}, t_{y}, \theta_{y a w}\right]\) 获得。
两步L-M优化得到相同的精度,计算时间可以减少约35%(表3)。
E.雷达建图
雷达建图以较低的频率运行,匹配 \(\left\{\mathbb{F}_{e}^{t}, \mathbb{F}_{p}^{t}\right\}\) 中的特征到点云地图 \(\overline{Q}^{t-1}\) 上,以优化位置变换。再用L-M方法得到最后的变换。
LeGO-LOAM的主要区别在于如何存储最终点云图:
保存每个单独的特征集 \(\left\{\mathbb{F}_{e}^{t}, \mathbb{F}_{p}^{t}\right\}\) ,而不是保存单个点云图。
例如, \(M^{t-1}=\left\{\left\{\mathbb{F}_{e}^{1}, \mathbb{F}_{p}^{1}\right\}, \ldots,\left\{\mathbb{F}_{e}^{t-1}, \mathbb{F}_{p}^{t-1}\right\}\right\}\) 表示以前所有特征集合的集合。每个 \(M^{t-1}\) 中的每个特征集合和雷达scan时pose相关联。
通过 \(M^{t-1}\) 得到 \(\overline{Q}^{t-1}\) 有两种方式:
第一种和Zhang Ji论文类似,选择在传感器视野里面的特征点集获得 \(\overline{Q}^{t-1}\) 。选择距离当前传感器位置100m以内的特征集合。选择的特征集合然后变换和融合到单个周围地图 \(\overline{Q}^{t-1}\) 。
第二种,在LeGO-LOAM中集成图优化方法。
1)图的节点:每个特征集合的传感器位姿。
特征集合 \(\left\{\mathbb{F}_{e}^{t}, \mathbb{F}_{p}^{t}\right\}\) 被看做为这个节点上的传感器测量数据。
2)雷达建图模型的位姿估计drift很低,假设在短时间内没有drift。通过选择一组近来的特征集合来构成 \(\overline{Q}^{t-1}\) ,例如 \(\overline{Q}^{t-1}=\left\{\left\{\mathbb{F}_{e}^{t-k}, \mathbb{F}_{p}^{t-k}\right\}, \ldots,\left\{\mathbb{F}_{e}^{t-1}, \mathbb{F}_{p}^{t-1}\right\}\right.\) (其中k表示 \(\overline{Q}^{t-1}\) 的大小)。
3)新节点和 \(\overline{Q}^{t-1}\) 中的已选节点之间加上空间约束(通过L-M优化得到的坐标变换)。
4)用loop closure进一步消除雷达建图的drift。如果用ICP发现当前特征集和先前特征集之间有匹配,则添加新约束。然后通过将姿势图发送到诸如[24](iSAM2)的优化系统来更新传感器的估计pose。
注意,只有第四节(D)中的实验使用此技术来创建其周围的地图。
4.实验
略
5.结论
略
参考文献
[1] P.J. Besl and N.D. McKay, “A Method for Registration of 3D Shapes,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 14(2): 239-256, 1992.
[2] S. Rusinkiewicz and M. Levoy, “Efficient Variants of the ICP Algorithm,” Proceedings of the Third International Conference on 3-D Digital Imaging and Modeling, pp. 145-152, 2001.
[3] Y. Chen and G. Medioni, “Object Modelling by Registration of Multiple Range Images,” Image and Vision Computing, vol. 10(3): 145-155, 1992.
[4] A. Segal, D. Haehnel, and S. Thrun, “Generalized-ICP,” Proceedings of Robotics: Science and Systems, 2009.
[5] R.A. Newcombe, S. Izadi, O. Hilliges, D. Molyneaux, D. Kim, A.J. Davison, P. Kohi, J. Shotton, S. Hodges, and A. Fitzgibbon, “KinectFusion: Real-time Dense Surface Mapping and Tracking,” Proceedings of the IEEE International Symposium on Mixed and Augmented Reality, pp. 127-136, 2011.
[6] A. Nuchter, “Parallelization of Scan Matching for Robotic 3D Mapping,” Proceedings of the 3rd European Conference on Mobile Robots, 2007.
[7] D. Qiu, S. May, and A. Nuchter, “GPU-Accelerated Nearest Neighbor Search for 3D Registration,” Proceedings of the International Conference on Computer Vision Systems, pp. 194-203, 2009.
[8] D. Neumann, F. Lugauer, S. Bauer, J. Wasza, and J. Hornegger, “Realtime RGB-D Mapping and 3D Modeling on the GPU Using the Random Ball Cover Data Structure,” IEEE International Conference on Computer Vision Workshops, pp. 1161-1167, 2011.
[9] R.B. Rusu, Z.C. Marton, N. Blodow, and M. Beetz, “Learning Informative Point Classes for the Acquisition of Object Model Maps,” Proceedings of the IEEE International Conference on Control, Automation, Robotics and Vision, pp. 643-650, 2008.
[10] R.B. Rusu, G. Bradski, R. Thibaux, and J. Hsu, “Fast 3D Recognition and Pose Using the Viewpoint Feature Histogram,” Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 2155-2162, 2010.
[11] Y. Li and E.B. Olson, “Structure Tensors for General Purpose LIDAR Feature Extraction,” Proceedings of the IEEE International Conference on Robotics and Automation, pp. 1869-1874, 2011.
[12] J. Serafin, E. Olson, and G. Grisetti, “Fast and Robust 3D Feature Extraction from Sparse Point Clouds,” Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 4105-4112, 2016.
[13] M. Bosse and R. Zlot, “Keypoint Design and Evaluation for Place Recognition in 2D Lidar Maps,” Robotics and Autonomous Systems, vol. 57(12): 1211-1224, 2009.
[14] R. Zlot and M. Bosse, “Efficient Large-scale 3D Mobile Mapping and Surface Reconstruction of an Underground Mine,” Proceedings of the 8th International Conference on Field and Service Robotics, 2012.
[15] B. Steder, G. Grisetti, and W. Burgard, ”Robust Place Recognition for 3D Range Data Based on Point Features,” Proceedings of the IEEE International Conference on Robotics and Automation, pp. 1400-1405, 2010.
[16] W.S. Grant, R.C. Voorhies, and L. Itti, “Finding Planes in LiDAR Point Clouds for Real-time Registration,” Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 4347-4354, 2013.
[17] M. Velas, M. Spanel, and A. Herout, “Collar Line Segments for Fast Odometry Estimation from Velodyne Point Clouds,” Proceedings of the IEEE International Conference on Robotics and Automation, pp. 4486-4495, 2016.
[18] R. Dube, D. Dugas, E. Stumm, J. Nieto, R. Siegwart, and C. Cadena,”SegMatch: Segment Based Place Recognition in 3D Point Clouds,” Proceedings of the IEEE International Conference on Robotics and Automation, pp. 5266-5272, 2017.
[19] J. Zhang and S. Singh, “LOAM: Lidar Odometry and Mapping in Real-time,” Proceedings of Robotics: Science and Systems, 2014.
[20] J. Zhang and S. Singh, “Low-drift and Real-time Lidar Odometry and Mapping,” Autonomous Robots, vol. 41(2): 401-416, 2017.
[21] A. Geiger, P. Lenz, and R. Urtasun, “Are We Ready for Autonomous Driving? The KITTI Vision Benchmark Suite”, Proceedings of theIEEE International Conference on Computer Vision and PatternRecognition, pp. 3354-3361, 2012.
[22] M. Himmelsbach, F.V. Hundelshausen, and H-J. Wuensche, “Fast Segmentation of 3D Point Clouds for Ground Vehicles,” Proceedings of the IEEE Intelligent Vehicles Symposium, pp. 560-565, 2010.
[23] I. Bogoslavskyi and C. Stachniss, “Fast Range Image-based Segmentation of Sparse 3D Laser Scans for Online Operation,” Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 163-169, 2016.
[24] M. Kaess, H. Johannsson, R. Roberts, V. Ila, J.J. Leonard, and F. Dellaert, “iSAM2: Incremental Smoothing and Mapping Using the Bayes Tree,” The International Journal of Robotics Research 31, vol. 31(2): 216-235, 2012.
[25] M. Quigley, K. Conley, B. Gerkey, J. Faust, T. Foote, J. Leibs, R. Wheeler, and A.Y. Ng, “ROS: An Open-source Robot Operating System,” IEEE ICRA Workshop on Open Source Software, 2009.