LeGO-LOAM中的数学公式推导

LeGO-LOAM是一种在LOAM之上进行改进的激光雷达建图方法，建图效果比LOAM要好，但是建图较为稀疏，计算量也更小了。

本文原地址：wykxwyc的博客

github注释后LeGO-LOAM源码：LeGO-LOAM_NOTED 关于代码的详细理解，建议阅读：

1.地图优化代码理解

2.图像重投影代码理解

3.特征关联代码理解

4.LeGO-LOAM中的数学公式推导

以上博客会随时更新，如果对你有帮助，请点击注释代码的github仓库右上角star按钮，你的鼓励将给我更多动力。

本文记录重新读LeGO-LOAM的代码时看到的数学运算，记录这些数学运算背后的原理，会随时更新。

featureAssociation中的数学公式
mapOptmization中的数学公式
transformFusion中的数学公式
参考文献及链接

featureAssociation中的数学公式

mapOptmization中的数学公式

cornerOptimization中的协方差矩阵计算

随机变量的协方差是什么?
1.在概率论和统计中，协方差是对两个随机变量联合分布线性相关程度的一种度量。两个随机变量越线性相关，协方差越大，完全线性无关，协方差为零。（线性无关并不代表完全无关，更不代表相互独立。）

2.两个随机变量 $X$ 与 $Y$ 协方差的定义如下：
$\operatorname{cov}(X, Y)=\mathrm{E}[(X-\mathrm{E}[X])(Y-\mathrm{E}[Y])] \tag{CO-1}$

如何判断两个随机变量的相关程度？
1.通过定义这两个变量之间的相关系数 $\eta$ 进行判断：
$\eta=\frac{\operatorname{cov}(X, Y)}{\sqrt{\operatorname{var}(X) \cdot \operatorname{var}(Y)}} \tag{CO-2}$

1表示完全线性相关，−1表示完全线性负相关，0表示线性无关。线性无关并不代表完全无关，更不代表相互独立。

样本的协方差矩阵
1.设多维随机变量 $\mathbf{X}=\left[X_{1}, X_{2}, X_{3}, \dots, X_{n}\right]^{T}$ 的协方差矩阵为 $\Sigma$ ,则协方差矩阵中的每个元素为:
$\Sigma_{i j}=\operatorname{cov}\left(X_{i}, X_{j}\right)=\mathrm{E}\left[\left(X_{i}-\mathrm{E}\left[X_{i}\right]\right)\left(X_{j}-\mathrm{E}\left[X_{j}\right]\right)\right] \tag{CO-3}$ 上式表示的是 $X_{i}$ 和 $X_{j}$ 之间的协方差。

公式CO-3也揭示了协方差矩阵中每个元素的计算过程，整个矩阵为： \(\begin{align} &\Sigma =\mathrm{E}\left[(\mathbf{X}-\mathrm{E}[\mathbf{X}])(\mathbf{X}-\mathrm{E}[\mathbf{X}])^{T}\right] \\ &=\left[\begin{array}{cccc}{\operatorname{cov}\left(X_{1}, X_{1}\right)} & {\operatorname{cov}\left(X_{1}, X_{2}\right)} & {\dots} & {\operatorname{cov}\left(X_{1}, X_{n}\right)} \\ {\operatorname{cov}\left(X_{2}, X_{1}\right)} & {\operatorname{cov}\left(X_{2}, X_{2}\right)} & {\dots} & {\operatorname{cov}\left(X_{2}, X_{n}\right)} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {\operatorname{cov}\left(X_{n}, X_{1}\right)} & {\operatorname{cov}\left(X_{n}, X_{2}\right)} & {\cdots} & {\operatorname{cov}\left(X_{n}, X_{n}\right)}\end{array}\right] \\ &=\left[\begin{array}{cccc}{\mathrm{E}\left[\left(X_{1}-\mathrm{E}\left[X_{1}\right]\right)\left(X_{1}-\mathrm{E}\left[X_{1}\right]\right)\right]} & {\mathrm{E}\left[\left(X_{1}-\mathrm{E}\left[X_{1}\right]\right)\left(X_{2}-\mathrm{E}\left[X_{2}\right]\right)\right]} & {\cdots} & {\mathrm{E}\left[\left(X_{1}-\mathrm{E}\left[X_{1}\right]\right)\left(X_{n}-\mathrm{E}\left[X_{n}\right]\right)\right]} \\ {\mathrm{E}\left[\left(X_{2}-\mathrm{E}\left[X_{2}\right]\right)\left(X_{1}-\mathrm{E}\left[X_{1}\right]\right)\right]} & {\mathrm{E}\left[\left(X_{2}-\mathrm{E}\left[X_{2}\right]\right)\left(X_{2}-\mathrm{E}\left[X_{2}\right]\right)\right]} & {\cdots} & {\mathrm{E}\left[\left(X_{2}-\mathrm{E}\left[X_{2}\right]\right)\left(X_{n}-\mathrm{E}\left[X_{n}\right]\right)\right]} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {\mathrm{E}\left[\left(X_{n}-\mathrm{E}\left[X_{n}\right]\right)\left(X_{1}-\mathrm{E}\left[X_{1}\right]\right)\right]} & {\mathrm{E}\left[\left(X_{n}-\mathrm{E}\left[X_{n}\right]\right)\left(X_{2}-\mathrm{E}\left[X_{2}\right]\right)\right]} & {\cdots} & {\mathrm{E}\left[\left(X_{n}-\mathrm{E}\left[X_{n}\right]\right)\left(X_{n}-\mathrm{E}\left[X_{n}\right]\right)\right]}\end{array}\right] \end{align}\) 记上面公式为(CO-4)。

2.样本的协方差矩阵的计算
样本集合为 $\left\{\mathbf{x}_{\cdot j}=\left[x_{1 j}, x_{2 j}, \ldots, x_{n j}\right]^{T} | 1 \leqslant j \leqslant m\right\}$ ，m表示样本数量。

整个样本的协方差矩阵：
\(\begin{align} &\hat{\Sigma} =\left[\begin{array}{cccc}{q_{11}} & {q_{12}} & {\cdots} & {q_{1 n}} \\ {q_{21}} & {q_{21}} & {\cdots} & {q_{2 n}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {q_{n 1}} & {q_{n 2}} & {\cdots} & {q_{n n}}\end{array}\right] \\ &=\frac{1}{m-1}\left[\begin{array}{cccc}{\sum_{j=1}^{m}\left(x_{1 j}-\overline{x}_{1}\right)\left(x_{1 j}-\overline{x}_{1}\right)} & {\sum_{j=1}^{m}\left(x_{1 j}-\overline{x}_{1}\right)\left(x_{2 j}-\overline{x}_{2}\right)} & {\cdots} & {\sum_{j=1}^{m}\left(x_{1 j}-\overline{x}_{1}\right)\left(x_{n j}-\overline{x}_{n}\right)} \\ {\sum_{j=1}^{m}\left(x_{2 j}-\overline{x}_{2}\right)\left(x_{1 j}-\overline{x}_{1}\right)} & {\sum_{j=1}^{m}\left(x_{2 j}-\overline{x}_{2}\right)\left(x_{2 j}-\overline{x}_{2}\right)} & {\cdots} & {\sum_{j=1}^{m}\left(x_{2 j}-\overline{x}_{2}\right)\left(x_{n j}-\overline{x}_{n}\right)} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {\sum_{j=1}^{m}\left(x_{n j}-\overline{x}_{n}\right)\left(x_{1 j}-\overline{x}_{1}\right)} & {\sum_{j=1}^{m}\left(x_{n j}-\overline{x}_{n}\right)\left(x_{2 j}-\overline{x}_{2}\right)} & {\cdots} & {\sum_{j=1}^{m}\left(x_{n j}-\overline{x}_{n}\right)\left(x_{n j}-\overline{x}_{n}\right)}\end{array}\right] \\ &=\frac{1}{m-1} \sum_{j=1}^{m}\left(\mathbf{x} ._{j}-\overline{\mathbf{x}}\right)\left(\mathbf{x}_{ : j}-\overline{\mathbf{x}}\right)^{T} \end{align}\) 记上面公式为CO-5。

LeGO-LOAM的代码中的协方差计算过程
1.LeGO-LOAM中的协方差采用公式OC-5中的计算方法,每个点云的维度为n=3,XYZ三个距离,一共有m=5个样本;
2.有一个区别就是代码中最后直接除以m=5，而公式OC-5中是除以m-1=4。

cornerOptimization中特征边缘的方向向量的计算

求方向向量的过程？
1.对识别为特征边缘的点计算它和它周围点的协方差矩阵，
2.然后用opencv库函数求解特征值和特征向量
3.会有一个大的特征值和两个小的特征值，大的特征值对应于方向向量。

为什么这个协方差矩阵的较大特征值对应的就是边缘的方向？

cornerOptimization中计算点到直线的距离

点指的是被认为是特征边缘上的点，直线就是特征边缘所在的这条直线。
简单来看就是计算点到直线的距离，用面积法进行计算。
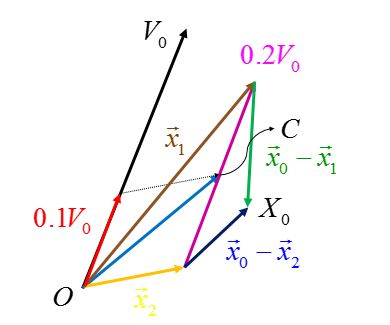
$conerOptmization$

在上图中，就是求点 $X_{0}$ 到紫色直线 $0.2V_{0}$ 的距离。

点 $X_{0}$ 对应于点pointSel，点 $C$ 对应于点 $[c_{x},c_{y},c_{z}]$ 先求绿色，蓝色线段构成的平行四边形面积，然后除以紫色的长度，得到距离值。

surfOptimization中如何计算点到平面的距离

pointAssociateToMap中对坐标变换的数学表达

这个函数中通过乘以旋转矩阵的方式，对坐标进行了变换，由局部坐标系变换到地图的全局坐标系。
变换是先进行yaw角的变换，然后是roll角的变换，最后是pitch的变换(即z->x->y),按照坐标变换左乘矩阵的规则，有： $\vec{p}_{o}=\mathbf{R}_{y}\mathbf{R}_{x}\mathbf{R}_{z} \vec{p}_{i}+\mathbf{T} \tag{PA-1}$

所以整体的旋转变换可以写成一个矩阵形式： $\mathbf{R}_{total}=\mathbf{R}_{y}\mathbf{R}_{x}\mathbf{R}_{z} \\ =Y_{1} X_{2} Z_{3}=\left[\begin{array}{ccc}{c_{1} c_{3}+s_{1} s_{2} s_{3}} & {c_{3} s_{1} s_{2}-c_{1} s_{3}} & {c_{2} s_{1}} \\ {c_{2} s_{3}} & {c_{2} c_{3}} & {-s_{2}} \\ {c_{1} s_{2} s_{3}-c_{3} s_{1}} & {c_{1} c_{3} s_{2}+s_{1} s_{3}} & {c_{1} c_{2}}\end{array}\right] \tag{PA-2}$

注意：上面公式简写了 $sin,cos$ 函数的符号。

已知roll，pitch，yaw三个角如何求得旋转矩阵？

旋转有两种，一种是向量旋转，另一张是坐标系旋转。如下图所示：

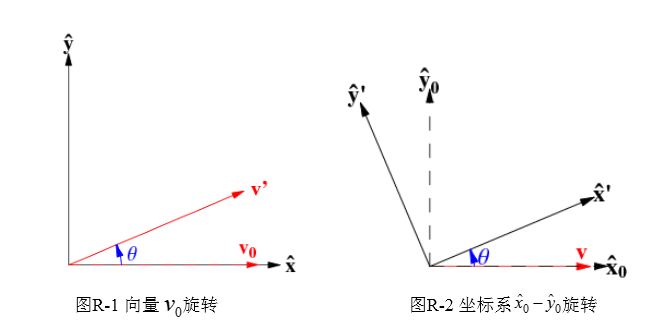
向量旋转
图R-1是向量旋转，通过平面几何公式，很容易就能得到旋转后的向量坐标是: $\mathbf{v}^{\prime}=\mathbf{R}_{\theta} \mathbf{v}_{0}= \left[\begin{array}{cc}{\cos \theta} & {-\sin \theta} \\ {\sin \theta} & {\cos \theta}\end{array}\right]\times \mathbf{v}_{0} \tag{RO-1}$ 其中有： $\mathrm{R}_{\theta}=\left[\begin{array}{cc}{\cos \theta} & {-\sin \theta} \\ {\sin \theta} & {\cos \theta}\end{array}\right] \tag{RO-2}$

坐标系旋转
坐标系旋转就是相当于向量的逆旋转，所以有： $\mathrm{R}_{\theta}^{\prime}=\left[\begin{array}{cc}{\cos \theta} & {\sin \theta} \\ {-\sin \theta} & {\cos \theta}\end{array}\right] \tag{RO-3}$

三维空间中的坐标旋转
公式RO-2可以看做是绕z轴正向旋转 $\theta$ 的角度，只有xy坐标变化，z坐标不变，对应于yaw角的旋转，按照这种方式我们可以分别得到绕roll，pitch和yaw角的旋转公式：
$\begin{array}{l}{\mathrm{R}_{x}(\alpha)=\left[\begin{array}{ccc}{1} & {0} & {0} \\ {0} & {\cos \alpha} & {\sin \alpha} \\ {0} & {-\sin \alpha} & {\cos \alpha}\end{array}\right]} \\ {\mathrm{R}_{y}(\beta)=\left[\begin{array}{ccc}{\cos \beta} & {0} & {-\sin \beta} \\ {0} & {1} & {0} \\ {\sin \beta} & {0} & {\cos \beta}\end{array}\right]} \\ {\mathrm{R}_{z}(\gamma)=\left[\begin{array}{ccc}{\cos \gamma} & {\sin \gamma} & {0} \\ {-\sin \gamma} & {\cos \gamma} & {0} \\ {0} & {0} & {1}\end{array}\right]}\end{array} \tag{RO-4}$ 注意上式中的绕y轴的pitch旋转和另外两个有点不同。

LeGO中的坐标旋转问题
LeGO中的局部坐标系下的点转换到全局坐标系中去的过程在pointAssociateToMap中对坐标变换的数学表达中以及说明,根据公式PA-2，我们可以得到pointAssociateToMap对点进行的坐标变换：
旋转(记为公式RO-5)：
$R=\left[\begin{array}{ccc}{cos_{ex} cos_{ez}+sin_{ex} sin_{ey} sin_{ez}} & {cos_{ez} sin_{ex} sin_{ey}-cos_{ex} sin_{ez}} & {cos_{ey} sin_{ex}} \\ {cos_{ey} sin_{ez}} & {cos_{ey} cos_{ez}} & {-sin_{ey}} \\ {cos_{ex} sin_{ey} sin_{ez}-cos_{ez} sin_{ex}} & {cos_{ex} cos_{ez} sin_{ey}+sin_{ex} sin_{ez}} & {cos_{ex} cos_{ey}}\end{array}\right]$

平移： $t=\left[ \begin{array}{ccc} t_{x} \\ t_{y} \\ t_{z}\end{array} \right]$

LMOptimization中如何进行优化迭代计算

先明确优化函数中的优化目标
优化函数优化的量是特征点与对应直线的距离(或者特征点与特征平面的距离)。
按照最优的情况下来说，特征点应该是在特征直线（或者特征平面）上的，所以距离应该为0.

但是当特征点到直线或者平面的距离不为0的时候，说明这个点由于运动产生了畸变，我们一开始估计的旋转 $R$ 和平移 $T$ 估计得不准确。所以对这个旋转和平移要进行调整。也就是每次优化后进行的如下操作：

transformTobeMapped[0] += matX.at<float>(0, 0);
transformTobeMapped[1] += matX.at<float>(1, 0);
transformTobeMapped[2] += matX.at<float>(2, 0);
transformTobeMapped[3] += matX.at<float>(3, 0);
transformTobeMapped[4] += matX.at<float>(4, 0);
transformTobeMapped[5] += matX.at<float>(5, 0);

其中的变换涉及到对旋转矩阵求雅克比，对距离求导等。

先明确一下优化中涉及到的定义
1.局部坐标系中的点 $X_{(k+1, i)}^{L}=(p x, p y, p z)^{T} \tag{LM-a}$ 这里的点是特征点，边缘上的点或者平面上的点，点i在LiDAR坐标系下,k+1时刻的坐标.

2.变换 $T_{(k+1)}^{w}$ 表示特征点经过这个变换内包含的3个旋转个3个平移，可以准确地变换到全局地图中，与地图中特征边缘和平面的距离为0；

3.将从局部坐标系变换到全局地图坐标系的变换定义成一个函数 $G( .)$ 这个函数将局部点 $X^{L}_{(k+1, i)}$ 转换到全局点 $X_{(k+1, i)}^{w}$ 。 $X_{(k+1, i)}^{w}=G\left(X_{(k+1, i)}^{L}, T_{(k+1)}^{w}\right)=R \cdot X_{(k+1, i)}^{L}+t \tag{LM-b}$

4.定义误差
$\text {loss}=d=D\left(X_{(k+1, i)}^{w}, map\right) \tag{LM-c}$

结合公式LM-b，LM-c
$\begin{align} & loss=d=D\left(X_{(k+1, i)}^{w}, map\right) \\ & =D\left(G\left(X_{(k+1, i)}^{L}, T_{(k+1)}^{w}\right), map\right) \\ & =D\left(R \cdot X_{(k+1, i)}^{L}+t, map\right) \\ \end{align} \tag{LM-d}$

5.误差对旋转求偏导的过程

\[\begin{array}{c} {\frac{\partial \operatorname{loss}}{\partial e x}=\frac{\partial D\left(G\left(X_{(k+1, i)}^{L}, T_{(k+1)}^{w}\right), map\right)}{\partial e x}} \\ {=\frac{\partial D( .)}{\partial G( .)} \cdot \frac{\partial G( .)}{\partial e x}}\\ {=\frac{\partial D( .)}{\partial G( .)} \cdot \frac{\partial\left(R \cdot X_{(k+1,1)}^{L}+t\right)}{\partial e x}}\\ {=\frac{\partial D( .)}{\partial G( .)} \cdot \frac{\partial\left(R \cdot X_{(k+1, i)}^{L}\right)}{\partial e x}+\frac{\partial D( .)}{\partial G( .)} \cdot \frac{\partial(t)}{\partial e x}} \\ {=\frac{\partial D( .)}{\partial G( .)} \cdot \frac{\partial\left(R \cdot X_{(k+1, i)}^{L}\right)}{\partial e x}} \end{array} \tag{LM-e}\]

6.误差对平移求偏导的过程

\[\begin{array}{c} {\frac{\partial \operatorname{loss}}{\partial x}=\frac{\partial D\left(G\left(X_{(k+1, i)}^{L}, T_{(k+1)}^{w}\right), map\right)}{\partial x}} \\ {=\frac{\partial D( .)}{\partial G( .)} \cdot \frac{\partial G( .)}{\partial x}}\\ {=\frac{\partial D( .)}{\partial G( .)} \cdot \frac{\partial\left(R \cdot X_{(k+1,1)}^{L}+t\right)}{\partial x}}\\ {=\frac{\partial D( .)}{\partial G( .)} \cdot \frac{\partial\left(R \cdot X_{(k+1, i)}^{L}\right)}{\partial x}+\frac{\partial D( .)}{\partial G( .)} \cdot \frac{\partial(t)}{\partial x}} \\ {=0+\frac{\partial D( .)}{\partial G( .)} \cdot \frac{\partial(t)}{\partial x}} \\ {=\frac{\partial D( .)}{\partial G( .)}} \end{array} \tag{LM-f}\]

7. $\frac{\partial D(\cdot)}{\partial G(\cdot)}$ 的求解
$\frac{\partial D( .)}{\partial G( .)}=\frac{\partial d}{\left(\partial X_{((k+1, i))}^{w}\right)} \tag{LM-g}$

公式LM-g中对全局坐标系中的点求导，可以理解成求一个全局点的移动方向，点在这个方向上移动， $d$ 减小得最快。

所以这个方向就是沿着垂线的方向。
所以点到直线的方向就是底边的垂线方向。
点到平面的方向就是平面的法线方向。

\[\frac{\partial D( .)}{\partial G( .)}=\frac{\partial d}{\left(\partial X_{((k+1, i))}^{w}\right)}=\left(\frac{\partial d}{\partial x},\frac{\partial d}{\partial y},\frac{\partial d}{\partial z}\right)=(la,lb,lc)\]

所以总结一下上面求解的两个部分：
$\begin{align} &\frac{\partial\left(R * X_{(k+1, i)}^{L}\right)}{\partial e x}=\frac{\partial\left(R \right)}{\partial e x}\cdot X_{(k+1, i)}^{L} \\ & =\frac{\partial\left(R \right)}{\partial e x}\cdot \left( p_x,p_y,p_z \right)^{T} \\ & =\left[\begin{array}{ccc}{sy \cdot cx \cdot sz} & {cz \cdot sy \cdot cx} & {-sx \cdot sy} \\ {-sx \cdot sz} & {-sx \cdot cz} & {-cx} \\ {cy \cdot cx \cdot sz} & {cy \cdot cz \cdot cx} & {-cy \cdot sx}\end{array}\right] \cdot \left( p_x,p_y,p_z\right)^T \end{align} \tag{LM-h}$

同样的做法可以求得 $\frac{\partial\left(R \times X_{(k+1, i)}^{L}\right)}{\partial e y}$ 以及 $\frac{\partial\left(R \times X_{(k+1, i)}^{L}\right)}{\partial e z}$ ,分别对应于代码中的ary和arz。

迭代计算的过程
代码中用的是高斯-牛顿法进行迭代计算求解的。高斯-牛顿法的基本形式为： $J^{T}J \Delta{x}=-J \cdot f(x)$

代码中，雅克比矩阵 $J$ 为matA, $matA=\left[\begin{array}{ccc} {\frac{\partial{d}}{\partial{roll}}} \\ {\frac{\partial{d}}{\partial{pitch}}} \\ {\frac{\partial{d}}{\partial{yaw}}} \\ {\frac{\partial{d}}{\partial{t_x}}} \\ {\frac{\partial{d}}{\partial{t_y}}} \\ {\frac{\partial{d}}{\partial{t_z}}} \\ \end{array} \right] \tag{matA}$

transformFusion中的数学公式

参考文献及链接

1.苦力笨笨的博客:https://www.cnblogs.com/terencezhou/p/6235974.html
2.知乎SLAM专栏-「能儿」的回答：https://zhuanlan.zhihu.com/p/57351961
3.mathworld.wolfram.com:http://mathworld.wolfram.com/RotationMatrix.html
4.维基百科旋转矩阵解释:https://en.wikipedia.org/wiki/Euler_angles#Definition_by_intrinsic_rotations

The math formula in LeGO-LOAM