目录
各种图算法的比较
| 算法名称 | 时间复杂度 | 空间复杂度 | 使用条件 |
|---|---|---|---|
| Dijstra | $O(V^2+E)/O(VlgV+ElgV)$ (最小堆) | $O(V)$ | 单源最短路径 |
| Floyd | \(O(V^3)\) | $O(V^2)$ | 多源最短路径 |
| Bellman-Ford | $O(VE)$ | $ O(V) $ | 单源最短路径 |
| SPFA | $O(VE)$ | $O(V)$ | 单源最短路径 |
DijkstraFloyd算法特点
1.通常用于求单源最短路径;
2.不允许图中带有负权值的边(也不允许有负权重的回路);
3.时间复杂度 $O(V^2+E)$ :所有的顶点都要被收录一次,所以外循环有 \(O(V)\) ,每一个循环里面又要扫描一遍,\(O(V^2)\);收集的过程中涉及到每个邻接点,每条边又被访问了一遍;
4.空间复杂度,存储到每个顶点的距离$O(V)$。
Floyd算法特点
1.通常用于求多源最短路径问题;
2.允许图中带有负权值的边(但不允许有负权重的环);
3.时间复杂度$O(V^3)$:挑选任意两个顶点对v$O(V^2)$ ,顶点对中间的节点$O(V)$,相乘;
4.空间复杂度$O(V^2)$:只存储每两个节点之间的距离以及路径;
Bellman-Ford算法特点
1.通常用于求单源最短路径;
2.允许图中带有负权值的边(但是不允许有负权重的回路);
3.时间复杂度 $O(VE)$ :最多会有 $V-1$ 层,每次遍历所有边进行更新 $O(E)$ ,相乘;
4.空间复杂度 $O(V)$ :只存储源点到所有点其他点的距离;
SPFA算法特点
1.通常用于求单源最短路径;
2.允许图中带有负权值的边(但是不允许有负权重的回路);
3.时间复杂度 $O(VE)$ :最差情况下是 $O(VE)$ ;
4.空间复杂度 $O(V)$ :只存储源点到所有点其他点的距离,队列大小最大也为 $V$ ;
Dijkstra算法
Dijkstra算法的输入输出
输入:整个网络拓扑和各链路的长度。
输出:源结点到网络中其他各结点的最短路径。
为什么Dijkstra不能有负权重的边?
在下面这个图中,从源点S到终点T用Dijkstra算法求出来的是边长为2,而不是边长为1.
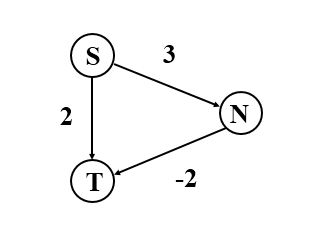
过程:从S开始,到N为3,到T为2,这步选择T;
然后找到V,但是T已经被加入到找到的点中去了,所以不再更新S到T的距离,因此不能找到边长为1(S->N->T)。
Dijkstra算法的运行过程
算法的大概过程为:从源节点开始,一步一步地寻找,每次找一个结点到源结点的最短路径,直到把所有的点都找到为止。
具体过程以图E-1的例子进行说明:
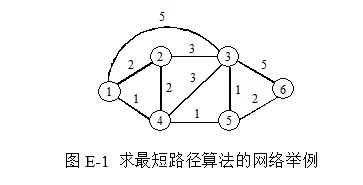
令 $D(v)$ 为源节点(图中的节点1)到某个节点 $v$ 的距离。
$l(i,j)$ 是节点 $i$ 到节点 $j$ 之间的距离。
算法只有两个部分:
1.初始化
令 $N$ 表示网络节点的集合。先令 $N={ 1 }$ 。然后对所有不在 $N$ 中的节点,进行更新。更新的过程为:
如果节点$v$与节点1直接相连, $D(v)=l(1,v)$ ;
如果节点 $v$ 与节点1不直接相连, $D(v)=\infty$ 。
2.更新下一个节点
寻找一个不在 $N$ 中的节点 $w$ ,其 $D(w)$ 值最小(如果有很多个值是一样的,可以任选一个)。把 $w$ 加入到 $N$ 中。然后对所有不在 $N$ 中的节点 $v$ ,用D(v)=min(D(v),D(w)+l(w,v))去更新原来的 $D(v)$ 值。
3.不断重复步骤2的过程,直到所有的节点都在 $N$ 中为止
对图E-1进行Dijkstra算法进行搜索的表格如下所示:
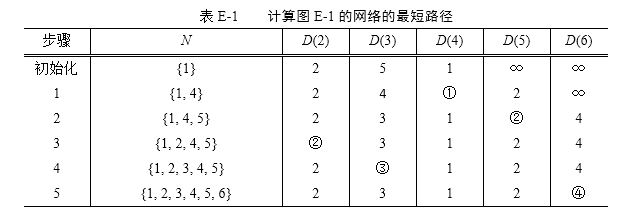
Dijkstra算法的C++实现
#include <bits/stdc++.h>
using namespace std;
/*
* vs -- 起始顶点(start vertex)
* prev -- 前驱顶点数组。
* dist -- 长度数组。
* mMatrix -- 图以邻接矩阵的形式进行表示
*/
void dijkstra(int vs, vector<vector<int>>& mMatrix,
vector<int>& dist,int mVexNum){
// flag[i]=1表示"顶点vs"到"顶点i"的最短路径已成功获取
// 节点号1-mVexNum
int flag[mVexNum+1];
// 初始化
for (int i = 1; i <=mVexNum; i++){
flag[i] = 0; // flag=0,没有被选中
dist[i] = mMatrix[vs][i]; // 顶点i的最短路径为"顶点vs"到"顶点i"的权。
}
// 对"顶点vs"自身进行初始化
flag[vs] = 1;
dist[vs] = 0;
// 遍历mVexNum-1次;每次找出一个顶点的最短路径
for (int i = 1; i < mVexNum; i++){
// 寻找当前最小的路径
// 即,在未获取最短路径的顶点中,找到离vs最近的顶点(k)
int min = INT_MAX;
int k=-1;
for (int j = 1; j <= mVexNum; j++){
if (flag[j]==0 && dist[j]<min){
min = dist[j];
k = j;
}
}
// 顶点k放入已经访问过的集合
flag[k] = 1;
// 即,当已经"顶点k的最短路径"之后,更新"未获取最短路径的顶点的最短路径和前驱顶点"
for (int j = 1; j <= mVexNum; j++) {
int tmp = (mMatrix[k][j]==INT_MAX ? INT_MAX : (min + mMatrix[k][j]));
if (flag[j] == 0 && (tmp < dist[j]) ){
dist[j] = tmp;
}
}
}
// 打印dijkstra最短路径的结果
for (int i = 1; i <= mVexNum; i++)
cout << "shortest(" <<vs<< ", " << i << ")=" << dist[i] << endl;
}
// 测试用例,一共有4个点,6条边,所有的边为
// 1->2,1
// 1->3,3
// 1->4,21
// 2->3,1
// 2->4,3;
// 3->4,1
int main(){
vector<vector<int>> graph={ {},
{0,0,1,3,21},
{0,INT_MAX,0,1,3},
{0,INT_MAX,INT_MAX,0,1},
{0,INT_MAX,INT_MAX,INT_MAX,INT_MAX} };
// 注意邻接矩阵没有用到graph[0]这一行
// graph只用到了4x4的矩阵
vector<int> dist(5,0);
dijkstra(1,graph,dist,4);
return 0;
}
Floyd算法
Floyd算法的输入输出
输入:整个网络拓扑和各链路的长度。
输出:图中每个节点到网络中其他各结点的最短路径。
Floyd算法的原理
Floyd算法全称为Floyd-Warshall算法。
Floyd-Warshall算法是解决任意两点间的最短路径的算法,可以处理有向图或负权值的最短路径问题,同时也被用于计算有向图的传递闭包(两个点是否连通)。
Floyd-Warshall算法的原理是动态规划。
若图G中有n个顶点的编号为1到n。
设 $D_{i,j,k}$ 为从 $i$ 到 $j$ 只以 $(1…k)$集合中的节点为中间节点的最短路径长度。
1.若最短路径经过点k,则 $D_{i,j,t}=D_{i,k,t-1} + D_{k,j,t-1}$ ;
2.若最短路径不经过点 $k$ ,则
\(D_{i,j,t}=D_{i,j,t-1}\)
。所以
\(D_{i,j,k}=min(D_{i,k,t-1}+D_{k,j,t-1})\)
,在实际算法中,可以在原空间上进行迭代,这样可以将空间降到二维。
Floyd算法的C++实现
// graph 是邻接矩阵表示的一个图
void Floyd( vector<vector<int>> graph,
vector<vector<int>>& dist,
vector<vector<int>>& path){
int n=graph.size();
for ( int i = 0; i < n; i++ ){
for( int j = 0; j < n; j++ ) {
dist[i][j] = graph[i][j];
path[i][j] = -1;
}
}
for( int k = 0; k < n; k++ ){
for(int i = 0; i < n; i++ ){
for( int j = 0; j < n; j++ ){
if( dist[i][k] + dist[k][j] < dist[i][j] ) {
dist[i][j] = dist[i][k] + dist[k][j];
path[i][j] = k;
}
}
}
}
}
Bellman-Ford算法
Bellman-Ford算法除了可求解边权均非负的单源点最短路径问题外,还能在更普遍的情况下(存在负权边)解决单源点最短路径问题。
Bellman-Ford算法的输入输出
输入:整个网络拓扑和各链路的长度(权重可以为负值)。
输出:源结点到网络中其他各结点的最短路径。最后,如果检测到有负权重的环,直接返回警告。
Bellman-Ford算法的原理
Bellman-Ford算法流程分为三个阶段:
1.初始化:
将除源点外的所有顶点的最短距离估计值0->d[s],INT_MAX->d[t];
2.迭代求解:
反复对边集E中的每条边进行松弛操作,使得顶点集V中的每个顶点v的最短距离估计值逐步逼近其最短距离;(运行 $|v|-1$ 次)
3.检验负权回路:
判断边集E中的每一条边的两个端点是否收敛。如果存在未收敛的顶点,则算法返回false,表明问题无解;
否则算法返回true,并且从源点可达的顶点v的最短距离保存在d[v]中。
注意点:
1.Bellman算法中,如果存在从源点可达的负权重回路,则最短路径不存在,因为可以重复走这个回路,使路径无穷小。
2.判断是否有负权重回路的方法:在进行了 $(V-1)$ 次更新之后,再来更新一次,如果还能够让某个路径最短,则说明有负权重的边存在。
3.Bellman-Ford算法是否一定要运行 $V-1$ 次?
运行次数可以少于 $V-1$ 次,在某次循环中,考虑每条边后,都没有改变当前源点到所有顶点的最短路径长度,那么算法就可以提前结束了。
4.Bellman-Ford算法的伪码描述:
BeLLMAN_FORD(G,w,s)
INTIALIZE-SINGLE-SOURCE(G,s) // 用图中与s相连的边进行初始化
for i=1 to |G.V|-1 // 循环V-1次
for each edge(u,v) in G.E // 边的循环,用于更新距离
RELAX(u,v,w)
for each edge(u,v) in G.E // 检查是否有负权重的环
if v.d > u.d+w(u,v)
return FALSE
return TRUE
Bellman-Ford算法的C++实现
# include <bits/stdc++.h>
using namespace std;
bool check(vector<vector<int>>& graph,vector<int>& dist,vector<int>& path,int vernum )
{
bool flag = true;
for( int i = 1; i <= vernum; ++i ){
for( int j = 1; j <= vernum; ++j ){
if( graph[i][j] != INT_MAX && dist[i] != INT_MAX &&
dist[j] >= dist[i] + graph[i][j] ){
if( dist[j] > dist[i] + graph[i][j] ){
flag = false;
dist[j] = dist[i] + graph[i][j];
path[j] = i;
}
}
}
}
// 最后一次如果返回flag=false,还能继续优化,说明存在负权环
return flag;
}
bool bellman( vector<vector<int>>& graph,vector<int>& dist,vector<int>& path,int vernum ){
// 在函数体内最多调用V-1次操作
for( int i = 0; i < vernum - 1; ++i ){
// 不能继续优化,提早结束,返回true
if( check(graph,dist,path,vernum)==true )
return true;
}
bool flag=check(graph,dist,path,vernum);
return flag;
}
// 测试用例,一共有4个点,6条边,所有的边为
// 1->2,1
// 1->3,3
// 1->4,21
// 2->3,1
// 2->4,3
// 3->4,1
int main(){
// 注意邻接矩阵没有用到graph[0]这一行
// graph只用到了4x4的矩阵
vector<vector<int>> graph={ {},
{0,0,1,3,21},
{0,INT_MAX,0,1,3},
{0,INT_MAX,INT_MAX,0,1},
{0,INT_MAX,INT_MAX,INT_MAX,INT_MAX}};
vector<int> path(5,-1);
vector<int> dist(5,INT_MAX);
dist[1]=0;
int vernum=4;
if( bellman(graph,dist,path,vernum)==true){
for( int i = 1; i <= vernum; ++i )
printf("%d%s", dist[i], i == vernum ? "\n":" ");
for( int i = 4; i != -1; i = path[i] )
printf("%d ", i);
}
else
printf("FALSE");
return 0;
}
SPFA算法
Shortest Path Faster Algorithm,简称SPFA算法。
算法是 Bellman-Ford算法 的队列优化算法的别称,通常用于求含负权边的单源最短路径,以及判负权环。
SPFA 最坏情况下复杂度和朴素 Bellman-Ford 相同,为 $O(VE)$ 。
SPFA算法的输入输出
和Bellman-Ford算法的输入输出一致。
输入:整个网络拓扑和各链路的长度(权重可以为负值)。
输出:源结点到网络中其他各结点的最短路径。最后,如果检测到有负权重的环,直接返回警告。
SPFA算法的原理
SPFA算法有点像广度优先搜索,每次不断扩大已经找到的范围。
SPFA算法的过程
约定加权有向图G不存在负权回路,即最短路径一定存在。
用数组d记录每个结点的最短路径估计值,用邻接表来存储图G。
我们采取的方法是动态逼近法:
1.设立一个先进先出的队列用来保存待优化的结点,优化时每次取出队首结点u。
2.用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作。
如果v点的最短路径估计值有所调整,且v点不在当前的队列中,就将v点放入队尾。
3.这样不断从队列中取出结点来进行松弛操作,直至队列空为止。
SPFA算法证明
每次将点放入队尾,都是经过松弛操作达到的。
因此,每次的优化将会有某个点v的最短路径估计值d[v]变小。
所以算法的执行会使d越来越小。
由于我们假定图中不存在负权回路,所以每个结点都有最短路径值。
因此,算法不会无限执行下去,随着d值的逐渐变小,直到到达最短路径值时,算法结束,这时的最短路径估计值就是对应结点的最短路径值。
实际上,如果一个点进入队列达到n次,则表明图中存在负环,没有最短路径。
SPFA算法的C++实现
#include<bits/stdc++.h>
using namespace std;
struct graph_table{
int vertex;
int weight;
graph_table(int x,int y) :
vertex(x), weight(y) {
}
};
/*
* 输入gt:邻接表
* dist : 与源点的距离值
* src : 源点
* n :一共有几个顶点
*/
int spfa(vector<vector<graph_table>>& gt,vector<int>& dist,int src,int n){
vector<int> visited(n+1,0);
// 初始化d数组,赋为无穷远
for(int i=1;i<=n;++i)
dist[i]=INT_MAX;
queue<int> q;
// 把源点k放入队列
q.push(src);
// 源点与源点的距离为0
dist[src]=0;
while(!q.empty()){
int u=q.front();q.pop();
int v;
visited[u]=0;
for(int i=0;i<gt[u].size();++i){
// 枚举所有的路径
v=gt[u][i].vertex;
if(dist[v]>dist[u]+gt[u][i].weight){
// src->v的距离大于 src->u->v,更新
dist[v] = dist[u]+gt[u][i].weight;
if(!visited[v]) {
q.push(v);
visited[v]=1;
}
}
}
}
for(int i=1;i<=n;++i)
cout<<dist[i]<<" ";
return 0;
}
int main(){
// 测试用例,一共有4个点,6条边,所有的边为
// 1->2,1
// 1->3,3
// 1->4,21
// 2->3,1
// 2->4,3;
// 3->4,1
/* !!!初始化邻接表时,一定要有n+1个*/
vector<vector<graph_table>> gt;
vector<graph_table> tmp;
gt.push_back(tmp);
// 节点1的邻接表
graph_table g1(2,1);
tmp.push_back(g1);
g1.vertex=3;g1.weight=3;
tmp.push_back(g1);
g1.vertex=4;g1.weight=21;
tmp.push_back(g1);
gt.push_back(tmp);
// 节点2
tmp.clear();
g1.vertex=3;g1.weight=1;
tmp.push_back(g1);
g1.vertex=4;g1.weight=3;
tmp.push_back(g1);
gt.push_back(tmp);
// 节点3
tmp.clear();
g1.vertex=4;g1.weight=1;
tmp.push_back(g1);
gt.push_back(tmp);
// 节点4
/* 少了以下两句,会出现数组越界,出现两次执行spfa函数 */
tmp.clear();
gt.push_back(tmp);
vector<int> dis(5,0);
spfa(gt,dis,1,4);
return 0;
}
参考文献
1.百度文库:link
2.浙江大学算法与数据结构课(陈越老师等)
3.博客网站:link
4.算法导论
5.百度百科:link
6.FireflyNo1的博客:link
7.Dijkstra算法介绍博客:link